题目内容
已知圆C:(x-a)2+(y-a)2=a2和直线l:3x+4y+3=0,若圆C上有且仅有两个点到l距离等于1,求a的取值范围.
思路解析：可以找一条和已知直线平行的直线与圆的交点与已知直线的距离为1,这样的直线如果存在,必须比较圆心到直线距离与半径的关系.
解：设与直线l平行且到l的距离为1的直线为3x+4y+c=0,则由两平行直线之间的距离公式可得
=1,∴c=-2或c=8.
由已知可得
＜|a|或
＜|a|.
整理可得|7a-2|＜5|a|或|7a+8|＜5|a|,即6a2-7a+1＜0或3a2+14a+8＜0，即
＜a＜1或-4＜a＜-
.
∴a的范围为
＜a＜1或-4＜a＜-
.
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
B.2-
C.
-1 D.
+1
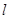:x-y+3=0,当直线
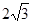时,则a=
:x-y+3=0,当直线
时,则a= 。