Question

（本小题满分12分）

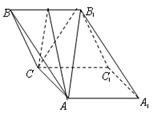
如图，斜三棱柱，已知侧面与底面垂直且，，，若二面角为，

（1）证明平面；                        

（2）求与平面所成角的正切值；

（3）在平面内找一点，使三棱锥为正三棱锥，并求点到平面距离.

Answer 1

（1）见解析

（2）

（3）

解析:

（1）　面面，因为面面＝，，所以面．                        （4分）

（2）取中点，连接，在中， 

是正三角形，，又面且面，

，即即为二面角的平面角为30°，        （6分）

 面，，在　中，，  

又面，即与面所成的线面角，

在中，    （8分）

　（3）在上取点，使，则因为是的中线，是的重心，在中，过作//交于， 面，//

面，即点在平面上的射影是的中心，该点即为所求，且，．    （12分）

注：用向量法做对同样给分