题目内容
12. 三棱锥P-ABC中,平面PAB⊥平面ABC,PA=PB=AB=$\frac{1}{2}$AC,∠BCA=30°.
三棱锥P-ABC中,平面PAB⊥平面ABC,PA=PB=AB=$\frac{1}{2}$AC,∠BCA=30°.(1)求证:BC⊥平面PAB;
(2)求二面角C-PA-B的余弦值.
分析 (1)证明AB⊥BC,利用平面与平面垂直的性质定理证明BC⊥平面PAB.
(2)取PA的中点D,连结BD,CD,说明∠CDB就是二面角C-PA-B的平面角,通过解三角形即可求出结果.
解答 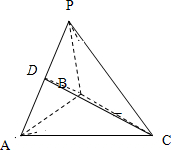 (1)证明:三棱锥P-ABC中,平面PAB⊥平面ABC,
(1)证明:三棱锥P-ABC中,平面PAB⊥平面ABC,
PA=PB=AB=$\frac{1}{2}$AC,∠BCA=30°.∴∠ABC=90°,∴AB⊥BC,
BC?平面ABC,∴BC⊥平面PAB.
(2)解:取PA的中点D,连结BD,CD,∵BC⊥平面PAB,PA=PB=AB,
∴BD⊥PA,∴PA⊥平面BCD,∴∠CDB就是二面角C-PA-B的平面角,
设AC=2,则PA=PB=AB=1,则BD=$\frac{\sqrt{3}}{2}$,BC=$\sqrt{3}$,
DC=$\sqrt{(\sqrt{3})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\frac{\sqrt{15}}{2}$.
cos∠CDB=$\frac{BD}{DC}$=$\frac{\frac{\sqrt{3}}{2}}{\frac{\sqrt{15}}{2}}$=$\frac{\sqrt{5}}{5}$.
∴二面角C-PA-B的余弦值为:$\frac{\sqrt{5}}{5}$.
点评 本题考查二面角的平面角的求法,平面与平面才知道判定与性质定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
7.高考复习经过二轮“见多识广”之后,为了研究考前“限时抢分”强化训练次数x与答题正确率y%的关系,对某校高三某班学生进行了关注统计,得到如下数据:
(1)求y关于x的线性回归方程,并预测答题正确率是100%的强化训练次数;
(2)若用$\frac{{y}_{i}}{{x}_{i}+3}$(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间[0,2)内,则强化训练有效,请问这个班的强化训练是否有效?
| x | 1 | 2 | 3 | 4 |
| y | 20 | 30 | 50 | 60 |
(2)若用$\frac{{y}_{i}}{{x}_{i}+3}$(i=1,2,3,4)表示统计数据的“强化均值”(精确到整数),若“强化均值”的标准差在区间[0,2)内,则强化训练有效,请问这个班的强化训练是否有效?
4.已知直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AB=2,CC1=2$\sqrt{2}$,E为CC1的中点,则点A到平面BED的距离为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
 某社区为该社区的小朋友举办了一次套圈活动,有A、B两个定点套圈位置,A、B两个定点前方各有6个不同编号的卡牌.如图所示的茎叶图记录着每个卡牌的编号.
某社区为该社区的小朋友举办了一次套圈活动,有A、B两个定点套圈位置,A、B两个定点前方各有6个不同编号的卡牌.如图所示的茎叶图记录着每个卡牌的编号. 如图,ABCD为梯形,PD⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°DC=2AB=2a,DA=$\sqrt{3}$A,PD=$\sqrt{3}$a,E为BC中点,连结AE,交BD于O.
如图,ABCD为梯形,PD⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°DC=2AB=2a,DA=$\sqrt{3}$A,PD=$\sqrt{3}$a,E为BC中点,连结AE,交BD于O.