题目内容
已知椭圆
 上的点到其两焦点距离之和为
上的点到其两焦点距离之和为 ,且过点
,且过点 .
.
(Ⅰ)求椭圆方程;
(Ⅱ)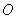 为坐标原点,斜率为
为坐标原点,斜率为 的直线过椭圆的右焦点,且与椭圆交于点
的直线过椭圆的右焦点,且与椭圆交于点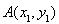 ,
,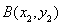 ,若
,若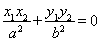 ,求△
,求△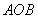 的面积.
的面积.
【答案】
(Ⅰ) (Ⅱ)1
(Ⅱ)1
【解析】
试题分析:(Ⅰ)由椭圆的定义及椭圆的几何性质易得 ,
,  ,即可得其椭圆方程。(Ⅱ)设出直线方程
,即可得其椭圆方程。(Ⅱ)设出直线方程 ,然后联立,消掉y(或x)得到关于x的一元二次方程,再根据韦达定理得出根与系数的关系式。先求出
,然后联立,消掉y(或x)得到关于x的一元二次方程,再根据韦达定理得出根与系数的关系式。先求出 再将
再将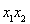 、
、 代入
代入 求得
求得 的值,由弦长公式求出
的值,由弦长公式求出 ,再用点到线的距离公式其点
,再用点到线的距离公式其点 到直线
到直线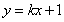 的距离,此距离即为△
的距离,此距离即为△ 底边
底边 上的高。用三角形面积公式可求得△
上的高。用三角形面积公式可求得△ 的面积。
的面积。
试题解析:解(Ⅰ)依题意有 ,
, .
.
故椭圆方程为 . 5分
. 5分
(Ⅱ)因为直线 过右焦点
过右焦点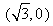 ,设直线
,设直线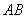 的方程为
的方程为  .
.
联立方程组
消去 并整理得
并整理得 . (*)
. (*)
故 ,
, .
.
 .
.
又 ,即
,即 .
.
所以 ,可得
,可得 ,即
,即  .
.
方程(*)可化为 ,由
,由 ,可得
,可得 .
.
原点 到直线
到直线 的距离
的距离 .
.
所以 . 13分
. 13分
考点:1椭圆的基础知识;2直线与椭圆的位置关系;3弦长公式;4点到直线的距离。

练习册系列答案
相关题目
 的左、右焦点分别为F1,F2,其右准线上l上存在点A(点A在x轴上方),使△AF1F2为等腰三角形.
的左、右焦点分别为F1,F2,其右准线上l上存在点A(点A在x轴上方),使△AF1F2为等腰三角形. 到两焦点F1,F2的距离之和为
到两焦点F1,F2的距离之和为 ,求△AF1F2的内切圆的方程.
,求△AF1F2的内切圆的方程.