题目内容
如图,在三棱柱ABC-A1B1C1中, CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.
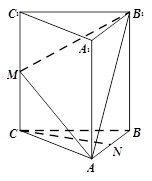
(1)求证:CN⊥AB1;
(2)求证:CN//平面AB1M.

(1)求证:CN⊥AB1;
(2)求证:CN//平面AB1M.
(1)如下(2)如下
试题分析:证明:(1)∵三棱柱ABC-A1B1C1中CC1⊥底面ABC,
∴BB1⊥平面ABC, ∴BB1⊥CN.
∵AC=BC,N是AB的中点,∴CN⊥AB.
又∵AB∩BB1=B,∴CN⊥平面AB B1A1,∴CN⊥AB1.
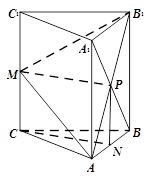
(2)(方法一)连结A1B交AB1于P.∵三棱柱ABC-A1B1C1,
∴P是A1B的中点.∵M,N分别是CC1,AB的中点,
∴NP // CM,且NP = CM,∴四边形MCNP是平行四边形,
∴CN//MP.∵CN
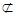 平面AB1M,MP
平面AB1M,MP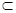 平面AB1M,
平面AB1M,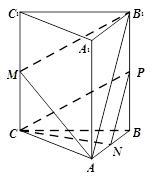
∴CN //平面AB1M.
(方法二)取BB1中点P,连结NP,CP.
∵N,P分别是AB,BB1的中点,∴NP //AB1.
∵NP
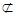 平面AB1M,AB1
平面AB1M,AB1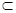 平面AB1M,
平面AB1M,∴NP //平面AB1M.同理 CP //平面AB1M.
∵CP∩NP =P,∴平面CNP //平面AB1M.
∵CN
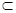 平面CNP,∴CN //平面AB1M.
平面CNP,∴CN //平面AB1M.点评:直线与平面平行、垂直的判定定理是常考知识点。在证明时,需结合定理的条件写,不可凭自己的主观意识去写。

练习册系列答案
相关题目
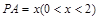 ,
,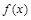 ,则函数
,则函数
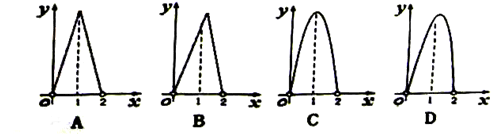
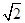 ,则 M 到面 ABC 的距离为( )
,则 M 到面 ABC 的距离为( )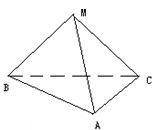
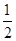
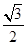
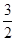
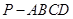 中,底面
中,底面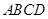 是正方形,侧面
是正方形,侧面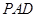
 底面
底面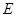 、
、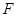 分别为
分别为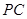 、
、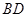 的中点.
的中点.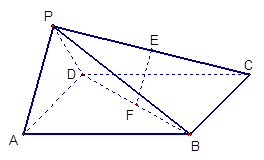
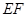 //平面
//平面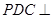 平面
平面 所在的平面与正方形
所在的平面与正方形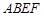 所在的平面相垂直,
所在的平面相垂直,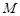 、
、 分别是
分别是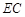 、
、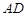 的中点.
的中点.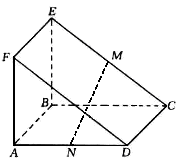
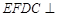 面
面 ;
;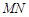 与平面
与平面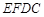 所成的角正弦值.
所成的角正弦值. 以及平面
以及平面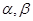 ,下面命题中正确的是
,下面命题中正确的是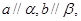 则
则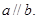
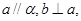 则
则
 则
则
 ,且
,且 ,则
,则
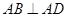 ,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD
,AD∥BC,AD =6,BC =4,AB =2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABCD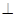 平面EFDC,设AD中点为P.
平面EFDC,设AD中点为P.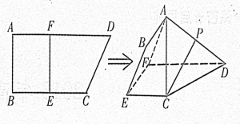
 的角,p为空间一定点,则过点p与
的角,p为空间一定点,则过点p与 A.,b所成的角都是50
A.,b所成的角都是50