题目内容
若函数y=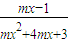
的定义域为R，则实数m的取值范围是 ．
【答案】分析：y=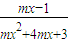
的定义域为R?mx2+4mx+3≠0恒成立，对m=0与m≠0两类讨论即可．
解答：解：∵y=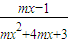
的定义域为R，
∴mx2+4mx+3恒不等于0．
∴当m=0时，mx2+4mx+3=3满足题意；
当m＞0时，△=16m2-12m＜0，
解得0＜m＜
，
当m＜0时，△=16m2-12m＜0，
m∈∅；
综上所述，0≤m＜
，即m∈[0，
）．
故答案为：m∈[0，
）．
点评：本题考查二次函数的性质，考查函数恒成立问题，考查分类讨论思想的应用，属于基础题．
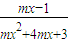的定义域为R?mx2+4mx+3≠0恒成立，对m=0与m≠0两类讨论即可．解答：解：∵y=
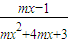的定义域为R，∴mx2+4mx+3恒不等于0．
∴当m=0时，mx2+4mx+3=3满足题意；
当m＞0时，△=16m2-12m＜0，
解得0＜m＜
，当m＜0时，△=16m2-12m＜0，
m∈∅；
综上所述，0≤m＜
，即m∈[0，）．故答案为：m∈[0，
）．点评：本题考查二次函数的性质，考查函数恒成立问题，考查分类讨论思想的应用，属于基础题．
练习册系列答案
相关题目
的定义域为R,则k的取值范围是______________.
的定义域为R,求实数m的取值范围.
的定义域为R,求实数k的取值范围.
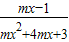的定义域为R，则实数m的取值范围是（ ）
）
，+∞）
）