题目内容
19．在x2＞x1＞0时，比较-$\frac{1}{a}+\frac{2}{{x}_{1}}$与-$\frac{1}{a}+\frac{2}{{x}_{2}}$的大小关系．分析 直接由函数$f（x）=-\frac{1}{a}+\frac{2}{x}$为（0，+∞）上的单调减函数得答案．
解答 解：∵$f（x）=-\frac{1}{a}+\frac{2}{x}$为（0，+∞）上的单调减函数，且x2＞x1＞0，
∴f（x2）＜f（x1），即$-\frac{1}{a}+\frac{2}{{x}_{1}}＜-\frac{1}{a}+\frac{2}{{x}_{2}}$．
故-$\frac{1}{a}+\frac{2}{{x}_{1}}$＜-$\frac{1}{a}+\frac{2}{{x}_{1}}$．
点评 本题考查不等式的大小比较，考查了函数单调性的性质，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
11．某电子广告牌连续播出四个广告，假设每个广告所需的时间互相独立，且都是整数分钟，经统计，以往播出100次所需的时间（t）的情况如下：
每次随机播出，若将频率视为概率．
（Ⅰ）求恰好在开播第6分钟后开始播出第3号广告的概率；
（Ⅱ）求第4分钟末完整播出广告1次的概率．
| 类别 | 1号广告 | 2号广告 | 3号广告 | 4号广告 |
| 广告次数 | 20 | 30 | 40 | 10 |
| 时间t（分钟/人） | 2 | 3 | 4 | 6 |
（Ⅰ）求恰好在开播第6分钟后开始播出第3号广告的概率；
（Ⅱ）求第4分钟末完整播出广告1次的概率．
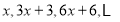的第四项等于（ ）