题目内容
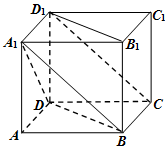
直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.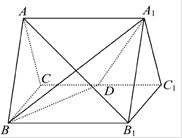
(1)求证:直线AB1⊥平面A1BD.
(2)求二面角A-A1D-B正弦值的大小.
(1)证明过程详见试题解析;(2)二面角A-A1D-B正弦值为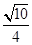 .
.
解析试题分析:(1)建立如下图的空间坐标系,要证直线AB1⊥平面A1BD,只需证明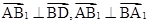
即可.(2)先求出平面A1AD的一个法向量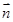 ,再用向量夹角公式求二面角A-A1D-B正弦值.
,再用向量夹角公式求二面角A-A1D-B正弦值.
试题解析:(1)取BC中点O,连接AO,
∵△ABC为正三角形,∴AO⊥BC,
∵直棱柱ABC-A1B1C1,∴平面ABC⊥平面BCC1B1且相交于BC,
∴AO⊥平面BCC1B1.取B1C1中点O1,则OO1∥BB1,∴OO1⊥BC.
以O为原点,如图建立空间直角坐标系O-xyz,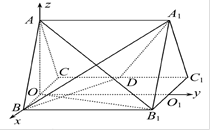
则B(1,0,0),D(-1,1,0),A1(0,2,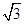 )A(0,0,
)A(0,0,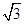 ),B1(1,2,0),C(-1,0,0),
),B1(1,2,0),C(-1,0,0),
∴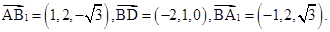
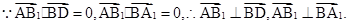
∴直线AB1⊥平面A1BD. 6分
(2)设平面A1AD的一个法向量为
n=(x,y,z).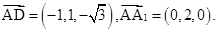
∵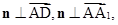
∴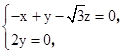 令z=1得n=(-
令z=1得n=(-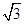 ,0,1)为平面A1AD的一个法向量.
,0,1)为平面A1AD的一个法向量.
由(1)知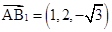 为平面A1BD的法向量.
为平面A1BD的法向量.
∴
∴二面角A-A1D-B正弦值的大小为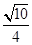 . 12分
. 12分
考点:空间向量、直线与平面的位置关系.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
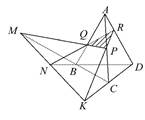
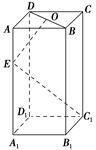
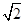 ,OE⊥EC1,求AA1的长.
,OE⊥EC1,求AA1的长.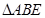 为直角三角形,
为直角三角形,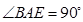 ,且
,且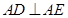 .
.
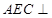 平面
平面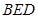 ;
;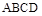 与
与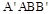 都是边长为
都是边长为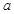 的正方形,点E是
的正方形,点E是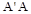 的中点,
的中点,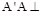 平面
平面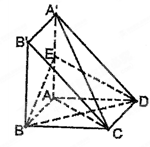
 平面
平面 ;
;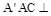 平面
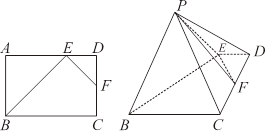
平面 中,点
中,点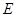 为边
为边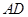 上的点,点
上的点,点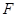 为边
为边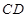 的中点,
的中点,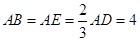 ,现将
,现将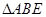 沿
沿 边折至
边折至 位置,且平面
位置,且平面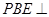 平面
平面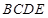 .
.
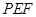 ;
;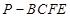 的体积.
的体积.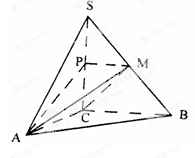
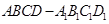 中,
中,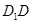
 底面
底面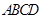 ,
,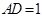 ,
,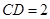 ,
,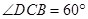 .
.
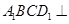 平面
平面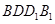 ;
;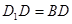 ,求四棱锥
,求四棱锥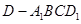 的体积.
的体积.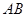 是圆的直径,
是圆的直径,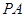 垂直圆所在的平面,
垂直圆所在的平面, 是圆上任一点,
是圆上任一点,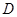 是线段
是线段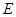 是线段
是线段 上的一点.
上的一点.
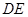 ∥平面
∥平面 ;
;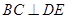 .
.