题目内容
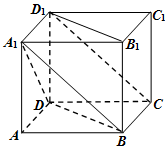
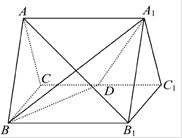
如图,在底面为平行四边形的四棱柱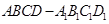 中,
中,
 底面
底面 ,
,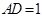 ,
,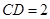 ,
,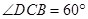 .
.
(Ⅰ)求证:平面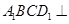 平面
平面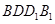 ;
;
(Ⅱ)若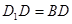 ,求四棱锥
,求四棱锥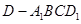 的体积.
的体积.
(Ⅰ)见解析(Ⅱ)1.
解析试题分析:(Ⅰ)首先由余弦定理求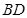 ,由勾股定理确定
,由勾股定理确定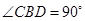 ,所以
,所以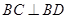 ,
,
结合条件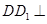 平面
平面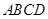 ,可知
,可知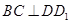 ,于是可证
,于是可证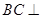 平面
平面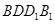 .
.
平面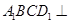 平面
平面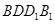 (Ⅱ)求四棱锥
(Ⅱ)求四棱锥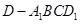 的体积有两个途径,第一,利用(Ⅰ)的结论平面
的体积有两个途径,第一,利用(Ⅰ)的结论平面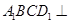 平面
平面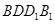 ,因为
,因为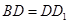 ,取
,取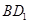 中点
中点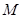 ,连结
,连结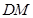 ,可证
,可证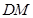 是四棱锥
是四棱锥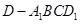 的高,从而求四棱锥
的高,从而求四棱锥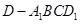 的体积;第二、因为
的体积;第二、因为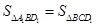 ,所以
,所以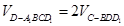 从而方便求解.
从而方便求解.
试题解析:(Ⅰ)证明: 在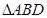 中,由余弦定理得:
中,由余弦定理得: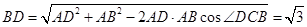 ,
,
所以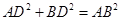 ,所以
,所以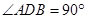 ,即
,即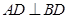 , 3分
, 3分
又四边形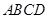 为平行四边形,所以
为平行四边形,所以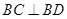 ,
,
又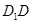
 底面
底面 ,
,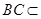 底面
底面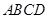 ,所以
,所以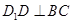 , 4分
, 4分
又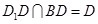 ,所以
,所以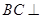 平面
平面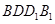 , 5分
, 5分
又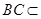 平面
平面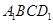 ,所以平面
,所以平面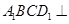 平面
平面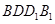 . 6分
. 6分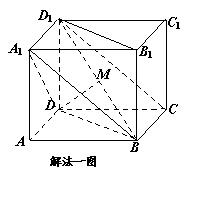
(Ⅱ)法一:连结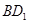 ,∵
,∵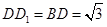 ,∴
,∴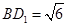
∵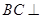 平面
平面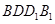 ,所以
,所以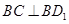 ,
,
所以四边形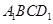 的面积
的面积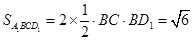 , 8分
, 8分
取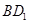 的中点
的中点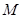 ,连结
,连结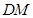 ,则
,则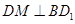 ,且
,且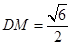 ,
,
又平面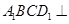 平面
平面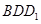 ,平面
,平面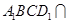 平面
平面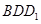
 ,
,
所以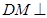 平面
平面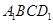 , 11分
, 11分
所以四棱锥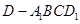 的体积:
的体积: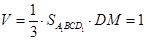 .
.

练习册系列答案
相关题目
 中
中 ,平面
,平面 外一条线段AB满足AB∥DE,AB
外一条线段AB满足AB∥DE,AB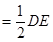 ,AB⊥AC,F是CD的中点.
,AB⊥AC,F是CD的中点.
 中,点
中,点 在平面ABC内的正投影分别为A,B,C,且
在平面ABC内的正投影分别为A,B,C,且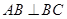 ,
, ,E为
,E为 中点,
中点,
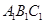 ,
,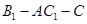 的大小.
的大小. 中, 底面四边形
中, 底面四边形 是直角梯形,
是直角梯形, 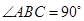 ,
,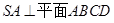 ,
, .
.
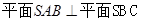 ;
; 与底面
与底面 中,
中,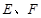 分别为
分别为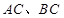 的中点.
的中点.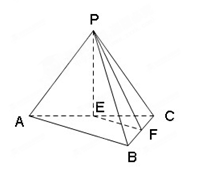
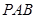 ;
;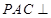 平面
平面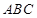 ,且
,且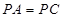 ,
,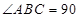 º,求证:平面
º,求证:平面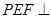 平面
平面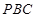
 .
.
 所在平面与正
所在平面与正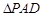 所在平面互相垂直,
所在平面互相垂直,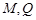 分别为
分别为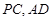 的中点.
的中点.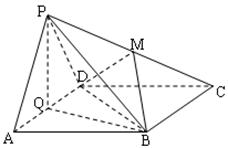
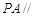 平面
平面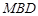 ;
;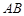 上是否存在一点
上是否存在一点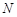 ,使得平面
,使得平面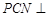 平面
平面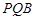 ?若存在,试指出点
?若存在,试指出点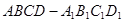 中,
中, ,
,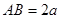 , E、
, E、  分别为
分别为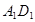 、
、 的中点.
的中点.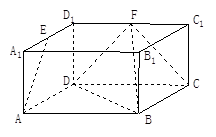
 平面
平面 ;
;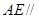 平面
平面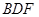 .
.