题目内容
 已知函数f(x)=x2-2|x|-1.
已知函数f(x)=x2-2|x|-1.(1)证明函数f(x)是偶函数;
(2)在如图所示的平面直角坐标系中作出函数f(x)的图象.
(3)根据图象求该函数的单调区间.
分析:(1)根据函数的定义域为R,且满足f(-x)=f(x),可得f(x)是偶函数.
(2)根据函数的解析式,画出函数f(x)图象如图所示.
(3)根据函数的图象可得,f(x)的单调区间.
(2)根据函数的解析式,画出函数f(x)图象如图所示.
(3)根据函数的图象可得,f(x)的单调区间.
解答: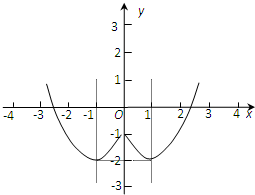 解:(1)∵x∈R,f(-x)=(-x)2-2|-x|-1=x2-2|x|-1=f(x),
解:(1)∵x∈R,f(-x)=(-x)2-2|-x|-1=x2-2|x|-1=f(x),
∴f(x)是偶函数.
(2)∵f(x)=
,函数f(x)图象如图所示.
(3)根据函数的图象可得,f(x)的单调增区间为[-1,0],[1,+∞);
f(x)的单调减区间为(-∞,-1],[0,1].
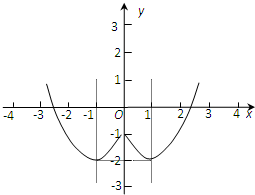 解:(1)∵x∈R,f(-x)=(-x)2-2|-x|-1=x2-2|x|-1=f(x),
解:(1)∵x∈R,f(-x)=(-x)2-2|-x|-1=x2-2|x|-1=f(x),∴f(x)是偶函数.
(2)∵f(x)=
|
(3)根据函数的图象可得,f(x)的单调增区间为[-1,0],[1,+∞);
f(x)的单调减区间为(-∞,-1],[0,1].
点评:本题主要考查函数的图象的作法,函数的单调性的判断和证明,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|