题目内容
已知函数f(x)=x3-x2+ax+b的图象在点P(0,f(0))处的切线方程为y=3x-2。
(I)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+ 是[2,+∞)上的增函数。
是[2,+∞)上的增函数。
(i)求实数m的最大值;
(ii)当m取最大值时,是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q 的坐标;若不存在,说明理由。
(I)求实数a,b的值;
(Ⅱ)设g(x)=f(x)+
 是[2,+∞)上的增函数。
是[2,+∞)上的增函数。(i)求实数m的最大值;
(ii)当m取最大值时,是否存在点Q,使得过点Q的直线若能与曲线y=g(x)围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q 的坐标;若不存在,说明理由。
解:(Ⅰ)由,f′(x)=x2-2x+a及题设得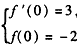
即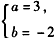 ;
;
(Ⅱ)(i)由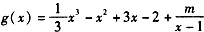 得
得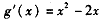
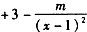
∵g(x)是[2,+∞)上的增函数
∴g'(x)≥0在[2,+∞)上恒成立
即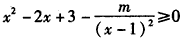 在
在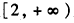 恒成立
恒成立
设(x-1)2=t
∵x∈[2,+∞)
∵t∈[1,+∞)
即不等式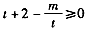 在
在 恒成立
恒成立
所以m≤t2+2t在[1,+∞)上恒成立
令y=t2+2t,t∈[1,+∞)
可得ymin=3,故m≤3,即m的最大值为3;
(ii)由(i)得
将函数g(x)的图像向左平移1个长度单位,再向下平移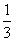 个长度单位,所得图像相应的函数解析式为
个长度单位,所得图像相应的函数解析式为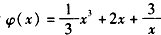
x∈(-∞,0)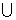 (0,+∞)
(0,+∞)
由于φ(-x)=-φ(x),所以φ(x)为奇函数,故φ(x)的图象关于坐标原点成中心对称,由此即得,函数g(x)的图象关于点 成中心对称
成中心对称
这也就表明,存在点 使得过点Q的直线若能与函数g(x)的图象围成两个封闭图形,则这两个封闭图形的面积总相等。
使得过点Q的直线若能与函数g(x)的图象围成两个封闭图形,则这两个封闭图形的面积总相等。
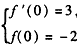
即
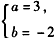 ;
;(Ⅱ)(i)由
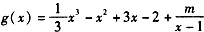 得
得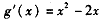
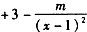
∵g(x)是[2,+∞)上的增函数
∴g'(x)≥0在[2,+∞)上恒成立
即
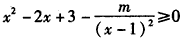 在
在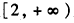 恒成立
恒成立设(x-1)2=t
∵x∈[2,+∞)
∵t∈[1,+∞)
即不等式
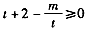 在
在 恒成立
恒成立所以m≤t2+2t在[1,+∞)上恒成立
令y=t2+2t,t∈[1,+∞)
可得ymin=3,故m≤3,即m的最大值为3;
(ii)由(i)得

将函数g(x)的图像向左平移1个长度单位,再向下平移
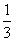 个长度单位,所得图像相应的函数解析式为
个长度单位,所得图像相应的函数解析式为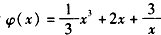
x∈(-∞,0)
 (0,+∞)
(0,+∞)由于φ(-x)=-φ(x),所以φ(x)为奇函数,故φ(x)的图象关于坐标原点成中心对称,由此即得,函数g(x)的图象关于点
 成中心对称
成中心对称这也就表明,存在点
 使得过点Q的直线若能与函数g(x)的图象围成两个封闭图形,则这两个封闭图形的面积总相等。
使得过点Q的直线若能与函数g(x)的图象围成两个封闭图形,则这两个封闭图形的面积总相等。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|