题目内容
设函数f(x)= ,其中向量
,其中向量 =(cos
=(cos ,sin
,sin ) (x∈R),向量
) (x∈R),向量 =(cos?,sin?)(|?|<
=(cos?,sin?)(|?|< ),f(x)的图象关于直线x=
),f(x)的图象关于直线x= 对称.
对称.
(Ⅰ)求?的值;
(Ⅱ)若函数y=1+sin 的图象按向量
的图象按向量 =(m,n) (|m|<π)平移可得到函数y=f(x)的图象,求向量
=(m,n) (|m|<π)平移可得到函数y=f(x)的图象,求向量 .
.
解:(Ⅰ)f(x)= =cos
=cos cos?+sin
cos?+sin sin?=cos(
sin?=cos( -?),
-?),
∵f(x)的图象关于直线x= 对称,
对称,
∴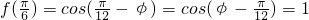 ,
,
∴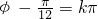 ,k∈Z,又|?|<
,k∈Z,又|?|< ,∴?=
,∴?= .
.
(Ⅱ)f(x)=cos( -
- )=sin(
)=sin( +
+ )=sin
)=sin (x+
(x+ ),
),
由y=1+sin 平移到y=sin
平移到y=sin (x+
(x+ ),只需向左平移
),只需向左平移 单位,
单位,
再向下平移1个单位,考虑到函数的周期为π,且 =(m,n) (|m|<π),
=(m,n) (|m|<π),
∴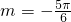 ,n=-1,即
,n=-1,即 =(-
=(- ,-1).
,-1).
另解:f(x)=cos( -
- )=sin(
)=sin( +
+ )=sin
)=sin (x+
(x+ ),
),
由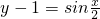 平移到
平移到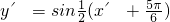 ,只要
,只要 即
即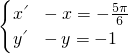 ,
,
∴ =(-
=(- ,-1).
,-1).
分析:(Ⅰ)通过向量的数量积,求出函数的关系式,利用对称轴直接求出?的值;
(Ⅱ)若函数y=1+sin 的图象按向量
的图象按向量 =(m,n) (|m|<π)平移,求出函数的解析式,利用与函数y=f(x)的图象相同,求向量
=(m,n) (|m|<π)平移,求出函数的解析式,利用与函数y=f(x)的图象相同,求向量 .另解:通过函数y=f(x)逆向推出函数,使得与函数y=1+sin
.另解:通过函数y=f(x)逆向推出函数,使得与函数y=1+sin 的图象相同,求出向量
的图象相同,求出向量 .
.
点评:本题是一道三角函数与平面向量相结合的综合问题,既考查了三角函数的变形以及三角函数的图象与性质,又考查了运用平面向量进行图象平移的知识.
 =cos
=cos cos?+sin
cos?+sin sin?=cos(
sin?=cos( -?),
-?),∵f(x)的图象关于直线x=
 对称,
对称,∴
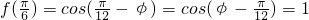 ,
,∴
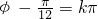 ,k∈Z,又|?|<
,k∈Z,又|?|< ,∴?=
,∴?= .
.(Ⅱ)f(x)=cos(
 -
- )=sin(
)=sin( +
+ )=sin
)=sin (x+
(x+ ),
),由y=1+sin
 平移到y=sin
平移到y=sin (x+
(x+ ),只需向左平移
),只需向左平移 单位,
单位,再向下平移1个单位,考虑到函数的周期为π,且
 =(m,n) (|m|<π),
=(m,n) (|m|<π),∴
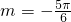 ,n=-1,即
,n=-1,即 =(-
=(- ,-1).
,-1).另解:f(x)=cos(
 -
- )=sin(
)=sin( +
+ )=sin
)=sin (x+
(x+ ),
),由
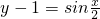 平移到
平移到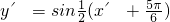 ,只要
,只要 即
即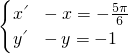 ,
,∴
 =(-
=(- ,-1).
,-1).分析:(Ⅰ)通过向量的数量积,求出函数的关系式,利用对称轴直接求出?的值;
(Ⅱ)若函数y=1+sin
 的图象按向量
的图象按向量 =(m,n) (|m|<π)平移,求出函数的解析式,利用与函数y=f(x)的图象相同,求向量
=(m,n) (|m|<π)平移,求出函数的解析式,利用与函数y=f(x)的图象相同,求向量 .另解:通过函数y=f(x)逆向推出函数,使得与函数y=1+sin
.另解:通过函数y=f(x)逆向推出函数,使得与函数y=1+sin 的图象相同,求出向量
的图象相同,求出向量 .
.点评:本题是一道三角函数与平面向量相结合的综合问题,既考查了三角函数的变形以及三角函数的图象与性质,又考查了运用平面向量进行图象平移的知识.

练习册系列答案
相关题目