题目内容
已知三棱锥S—ABC的底面是正三角形,A点在侧面SBC上的射影H是△SBC的垂心.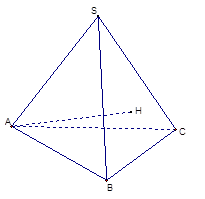
(1)求证:BC⊥SA
(2)若S在底面ABC内的射影为O,证明:O为底面△ABC的中心;
(3)若二面角H—AB—C的平面角等于30°,SA=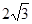 ,求三棱锥S—ABC的体积.
,求三棱锥S—ABC的体积.
(1)先证明 (2) 先证O为底面△ABC的垂心 (3)
(2) 先证O为底面△ABC的垂心 (3)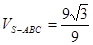
解析试题分析:证明:(1) 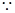 AH⊥面SBC,BC在面SBC内 ∴AH⊥BC
AH⊥面SBC,BC在面SBC内 ∴AH⊥BC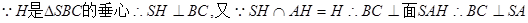

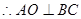 ,同理
,同理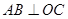 ,因此
,因此
O为底面△ABC的垂心,而三棱锥S—ABC的底面是正三角形,故O为底面△ABC的中心
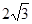 ,设CO交AB于F,则CF⊥AB, CF是EF在面ABC内的射影,
,设CO交AB于F,则CF⊥AB, CF是EF在面ABC内的射影,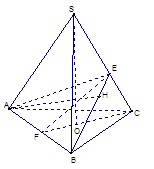
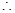 EF⊥AB,
EF⊥AB,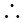 ∠EFC为二面角H—AB—C的平面角,∠EFC=30°,∠ECF=60°,
∠EFC为二面角H—AB—C的平面角,∠EFC=30°,∠ECF=60°,OC=
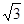 ,SO=3,AB=3,
,SO=3,AB=3,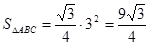

考点:直线与平面垂直的性质;棱柱、棱锥、棱台的体积.
点评:本题考查异面直线垂直的证明,考查三角形中心的证明,考查三棱锥体积的求法,解题时要认真审题,仔细解答,合理地化空间问题为平面问题.

练习册系列答案
相关题目
 中,侧面
中,侧面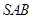 与侧面
与侧面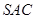 均为等边三角形,
均为等边三角形, 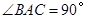 ,
,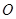 为
为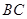 中点.
中点.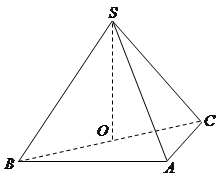
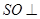 平面
平面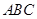 ;
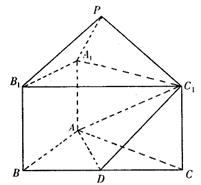
;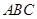 为正三角形的直三棱柱
为正三角形的直三棱柱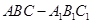 中,
中,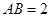 ,
,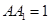 ,
, 是
是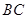 的中点,点
的中点,点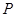 在平面
在平面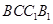 内,
内, .
. 
 ;
;  ∥平面
∥平面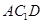 ;
;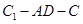 的大小.
的大小.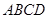 与
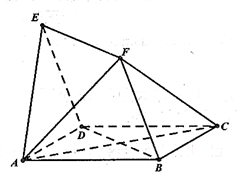
与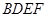 均为菱形,
均为菱形,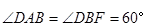 ,且
,且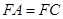 .
.
 ;
;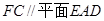 ;
;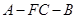 的余弦值.
的余弦值. 的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,
的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱, ,
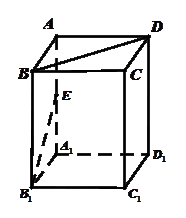
,
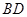 与B1E所成角的大小;
与B1E所成角的大小;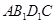 的体积.
的体积. 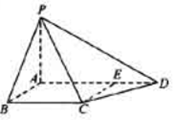
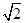 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积 ,如图二,在二面角
,如图二,在二面角
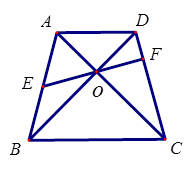
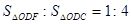
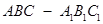 中,△
中,△ 是边长为
是边长为 的等边三角形,
的等边三角形, 平面
平面 ,
, 分别是
分别是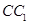 ,
, 的中点.
的中点. 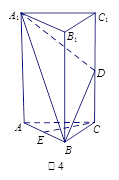
 ∥平面
∥平面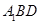 ;
; 为
为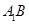 上的动点,当
上的动点,当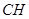 与平面
与平面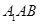 所成最大角的正切值为
所成最大角的正切值为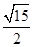 时,
时,