题目内容
中，
分别是
的对边，下列条件
①
； ②
；
③
； ④
能唯一确定的有____________________（写出所有正确答案的序号）
②③④
解析试题分析：①当时，由正弦定理可得
，且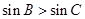
，故满足条件的
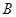可能是锐角，也可能是钝角，故满足①的三角形有两个；②当时，满足任意两边之和大于第三边，由于此三角形三边为定值，故这样的三角形只有一个；③由，可得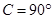
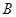，此直角三角形的三内角和斜边是确定的，故只有唯一的一个；④当时，利用正弦定理以及大边对大角可得是一个固定的锐角，故
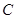就确定了，此三角形确定了三个内角和其中的两边，故这样的三角形只有一个故填②③④．
考点：1、正弦定理；2、三角形三边的关系；3、三角形的形状的判断．
练习册系列答案
相关题目
恒成立；②在三角形ABC中，如果有sinA=sinB成立，则必有A=B；③将两个变量所对应的点在平面直角坐标系中描出来，如果所描的点在散点图中没有显示任何关系则称变量间是不相关的；④等差数列{an}的首项a1=-50，公差d=2，前n项和为Sn，则n=25或n=26是使Sn取到最大值；其中为正确命题的序号是： .
,则
=______.
，AC=1，以AB为边作等腰直角三角形ABD（B为直角顶点，C、D两点
变化时，线段CD长的最大值为 ．
，则DABC的形状一定为___________.
BD，BC＝2BD，则sinC的值为________．
,n=
,m⊥n,且a=2,cosB=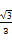
,则b=________.
中，
，则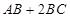
的最大值为 。
，与观测站A距离 
海里的B处有一货船正匀速直线行驶，半小时后，又测得该货船位于观测站A东偏北 
的C处，且
，已知A、C两处的距离为10海里，则该货船的船速为海里／小时___________．