题目内容
【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径 | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)由以往统计数据知,设备的性能根据以下不等式进行评判(![]() 表示相应事件的概率);①
表示相应事件的概率);①![]() ;②
;②![]() ;③
;③![]() ,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.为评判一台设备
,评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁.为评判一台设备![]() 的性能,从该设备加工的零件中任意抽取一件,记其直径为
的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,试判断设备
,试判断设备![]() 的性能等级
的性能等级
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
(i)若从设备![]() 的生产流水线上随意抽取2件零件,求恰有一件次品的概率;
的生产流水线上随意抽取2件零件,求恰有一件次品的概率;
(ii)若从样本中随意抽取2件零件,计算其中次品个数![]() 分布列和数学期望
分布列和数学期望![]() .
.
【答案】(1)该设备![]() 的性能为丙级别(2)(i)
的性能为丙级别(2)(i)![]() (ii)详见解析,
(ii)详见解析,![]()
![]()
【解析】
(1)通过计算可得答案;
(2)(i)根据独立重复事件的概率公式计算可得答案;(ii)根据二项分布的概率公式计算可得分布列,根据期望公式即可得期望.
(1)由题意知道:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以由图表知道:![]() ,
,
![]() ,
,
![]() ,
,
所以该设备![]() 的性能为丙级别;
的性能为丙级别;
(2)由图表知道:直径小于或等于![]() 的零件有2件,大于
的零件有2件,大于![]() 的零件有4件,共计6件.
的零件有4件,共计6件.
(i)从设备![]() 的生产流水线上任取一件,取到次品的概率为
的生产流水线上任取一件,取到次品的概率为![]() ,所以恰有一件次品的概率为
,所以恰有一件次品的概率为![]() (或等于0.1128);
(或等于0.1128);
(ii)从100件样品中任意抽取2件,次品数![]() 可能取值为0,1,2,
可能取值为0,1,2,
![]() ,
,![]() ,
,![]() .
.
所以,随机变量![]() 的分布列为
的分布列为
| 0 | 1 | 2 |
|
|
|
|
故![]() .
.

 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制如图所示频率分布直方图,已知中间三组的人数可构成等差数列.
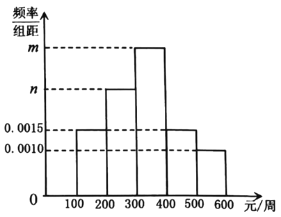
(1)求![]() 的值;
的值;
(2)分析人员对100名调查对象的性别进行统计发现,消费金额不低于300元的男性有20人,低于300元的男性有25人,根据统计数据完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为消费金额与性别有关?
的把握认为消费金额与性别有关?
(3)分析人员对抽取对象每周的消费金额![]() 与年龄
与年龄![]() 进一步分析,发现他们线性相关,得到回归方程
进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
![]() 列联表
列联表
男性 | 女性 | 合计 | |
消费金额 | |||
消费金额 | |||
合计 |
临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()