题目内容
1.若等差数列{an}中,满足a4+a6+a2010+a2012=8,则S2015=4030.分析 利用等差数列的通项公式性质及其前n项和公式即可得出
解答 解:∵a2012+a4=a6+a2010=a1+a2015,
a4+a6+a2010+a2012=8,
∴2(a1+a2015)=8,
∴a1+a2015=4,
∴S2015=$\frac{2015({a}_{1}+{a}_{2015})}{2}$=4030.
故答案为:4030.
点评 本题考查了等差数列的通项公式性质及其前n项和公式,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
13.设复数z1=l+2i,z2=l-ai,若z1•z2为实数,则实数a=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14.已知$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(x,1),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则x=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
16.已知集合M={x∈R|x2-x=0},N={x|x=2n+1,n∈Z},则M∩N为( )
| A. | {0} | B. | {0,1} | C. | {1} | D. | ∅ |
6.设实数x,y满足$\left\{\begin{array}{l}y≤2x+2\\ x+y-2≥0\\ x≤2\end{array}\right.$,则$\frac{y-1}{x+3}$的取值范围是( )
| A. | $(-∞,-\frac{1}{5}]∪[1,+∞)$ | B. | $[\frac{1}{3},1]$ | C. | $[-\frac{1}{5},\frac{1}{3}]$ | D. | $[-\frac{1}{5},1]$ |
 的算法,画出流程图,并写出伪代码.
的算法,画出流程图,并写出伪代码. 在
在 上是
上是 的减函数,则
的减函数,则 的取值范围是( )
的取值范围是( ) B.
B.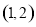
 D.
D.