题目内容
16.已知集合M={x∈R|x2-x=0},N={x|x=2n+1,n∈Z},则M∩N为( )| A. | {0} | B. | {0,1} | C. | {1} | D. | ∅ |
分析 化简M={x∈R|x2-x=0}={0,1},从而求M∩N.
解答 解:M={x∈R|x2-x=0}={0,1},
故M∩N={x|x=2n+1,n∈Z}={1},
故选;C.
点评 本题考查了集合的化简与运算,属于基础题.

练习册系列答案
相关题目
8.正项等比数列{an}满足:a3=a2+2a1,若存在am,an,使得am•an=16a12,则$\frac{1}{m}+\frac{9}{n}$的最小值为( )
| A. | 2 | B. | 16 | C. | $\frac{8}{3}$ | D. | $\frac{3}{2}$ |
9.设△ABC的内角A,B,C所对的边分别是a,b,c,若AB边上的高为$\frac{c}{2}$,且a2+b2=2$\sqrt{2}$ab,则C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
11.记函数f(x)的导函数为f′(x),若f(x)对应的曲线在点(x0,f(x0))处的切线方程为y=-x+1,则( )
| A. | f′(x0)=2 | B. | f′(x0)=1 | C. | f′(x0)=0 | D. | f′(x0)=-1 |
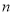 的值是( )
的值是( )
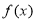 是定义在
是定义在 上以2为周期的奇函数,当
上以2为周期的奇函数,当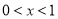 时,
时,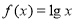 ,设
,设 ,
,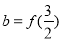 ,
, ,则( )
,则( ) B.
B.
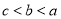 D.
D.