题目内容
设Q是圆O′:(x+1)2+y2=8上的动点,F是抛物线y2=4x的焦点,线段FQ的垂直平分线l交半径O′Q于点P.
(1)求点P的轨迹C的方程;
(2)斜率为k的直线l过点(0,
)且与轨迹C交于不同的两点A,B,记△AB0的面积为S=f(k),若
•
=m(
≤m≤
),求f(k)的最大值和最小值.
(1)求点P的轨迹C的方程;
(2)斜率为k的直线l过点(0,
| k2+1 |
| OA |
| OB |
| 3 |
| 5 |
| 3 |
| 4 |
分析:(1)由题意可得|PO′|+|PQ|=R,又|PQ|=|PF|,所以得到P点的轨迹为椭圆,且可知a,c的值,代入b2=a2-c2求出b的值,则椭圆方程可求;
(2)设出直线方程,为方便可令t=
,和椭圆方程联立,化为关于x的一元二次方程,得到直线和椭圆两个焦点的横坐标的和与积,代入数量积
•
=m后得到k与m的关系,利用原题给出的m的范围求得k的范围,
由弦长公式求出|AB|,由点到直线的距离公式求出O到直线的距离,代入三角形的面积公式后化为关于k的函数式,化简整理后利用单调性求最值.
(2)设出直线方程,为方便可令t=
| k2+1 |
| OA |
| OB |
由弦长公式求出|AB|,由点到直线的距离公式求出O到直线的距离,代入三角形的面积公式后化为关于k的函数式,化简整理后利用单调性求最值.
解答:解:(1)O′(-1,0),半径R=2
,因为线段FQ的垂直平分线l交半径O′Q于点O,连结PF,
所以|PQ|=|PF|,|PO′|+|PQ|=R,故|PO′|+|PF|=2
(2
>2=|O′F|),
由椭圆的定义,点P的轨迹是以O′,F为焦点的椭圆,设其方程为
+
=1(a>b>0),
则a=
,c=1,b2=a2-c2=1.
故点P的轨迹C的方程是
+y2=1;
(2)设斜率为k的直线的方程为y=kx+t,其中t=
.
设A(x1,y1),B(x2,y2),则
由
,消去y得(2k2+1)x2+4ktx+2t2-2=0.
又△=8k2>0(k≠0),所以x1+x2=-
,x1x2=
.
则
•
=x1x2+y1y2=x1x2+(kx1+t)(kx2+t)
=(1+k2)x1x2+tk(x1+x2)+t2
=
.
故
=m.因为
≤m≤
,所以
≤
≤
,
所以
≤k2≤2,
由弦长公式得:|AB|=
•
=
•
.
原点O到直线y=kx+t的距离d=
=
=1.
所以f(k)=S=
|AB|•d=
•
=
=
.
在[
,2]上是k2的增函数,故当k2=
时,f(k)min=
;当k2=2时,f(x)max=
.
| 2 |
所以|PQ|=|PF|,|PO′|+|PQ|=R,故|PO′|+|PF|=2
| 2 |
| 2 |
由椭圆的定义,点P的轨迹是以O′,F为焦点的椭圆,设其方程为
| x2 |
| a2 |
| y2 |
| b2 |
则a=
| 2 |
故点P的轨迹C的方程是
| x2 |
| 2 |
(2)设斜率为k的直线的方程为y=kx+t,其中t=
| k2+1 |
设A(x1,y1),B(x2,y2),则
由
|
又△=8k2>0(k≠0),所以x1+x2=-
| 4kt |
| 2k2+1 |
| 2t2-2 |
| 2k2+1 |
则
| OA |
| OB |
=(1+k2)x1x2+tk(x1+x2)+t2
=
| k2+1 |
| 2k2+1 |
故
| k2+1 |
| 2k2+1 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| k2+1 |
| 2k2+1 |
| 3 |
| 4 |
所以
| 1 |
| 2 |
由弦长公式得:|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+k2 |
2
| ||
| 2k2+1 |
原点O到直线y=kx+t的距离d=
| |t| | ||
|
| ||
|
所以f(k)=S=
| 1 |
| 2 |
| k2+1 |
| ||
| 2k2+1 |
=
|
|
在[
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
2
| ||
| 5 |
点评:本题考查了轨迹方程,考查了直线与圆锥曲线的关系,考查了数量积在解题中的应用,涉及直线与圆锥曲线的关系问题,经常利用直线与圆锥曲线联立,借助于一元二次方程的根与系数关系解题,避免了更为繁杂的运算,是解决该类问题的常用方法,考查了学生的计算能力,属压轴题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
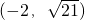 作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.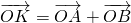 ,求
,求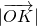 的最小值(O为坐标原点).
的最小值(O为坐标原点). 作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.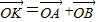 ,求
,求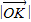 的最小值(O为坐标原点).
的最小值(O为坐标原点).