题目内容
过点Q 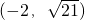 作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
(1)求r的值;
(2)设P是圆O上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设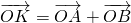 ,求
,求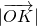 的最小值(O为坐标原点).
的最小值(O为坐标原点).
(3)从圆O外一点M(x1,y1)向该圆引一条切线,切点为T,N(2,3),且有|MT|=|MN|,求|MT|的最小值,并求此时点M的坐标.
解:(1)圆C:x2+y2=r2(r>0)的圆心为O(0,0),则
∵过点Q(-2, ) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4
) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4
∴r=OD=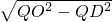 =
=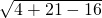 =3;
=3;
(2)设直线l的方程为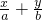 =1(a>0,b>0),即bx+ay-ab=0,则A(a,0),B(0,b),
=1(a>0,b>0),即bx+ay-ab=0,则A(a,0),B(0,b),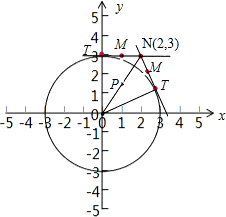
∵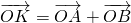 ,∴
,∴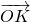 =(a,b),∴|
=(a,b),∴|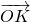 |=
|=
∵直线l与圆C相切,∴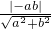 =3
=3
∴3 =ab≤
=ab≤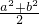
∴a2+b2≥36
∴|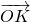 |≥6
|≥6
当且仅当a=b=3 时,|
时,|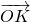 |的最小值为6.
|的最小值为6.
(3)∵切线MN⊥OT,∴|MT|2=|MO|2-9,又|MN|=|MT|,∴|MN|2=|MO|2-9,
M(x1,y1),过N(2,3)的直线的斜率为k,所以NT的方程为:y-3=k(x-2),
与圆的方程x2+y2=9联立,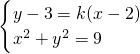 ,消去y可得:(k2+1)x2+2(3-2k)kx+4k2-12k=0,
,消去y可得:(k2+1)x2+2(3-2k)kx+4k2-12k=0,
因为直线与圆相切,所以△=0,即[2(3-2k)k]2-4(k2+1)(4k2-12k)=0,
化简得:5k2+12k=0,解得k=0或k=- ,
,
当k=0时,x=0,此时T(0,3),当k= 时,x=
时,x= ,此时T(
,此时T( ,
, )
)
∴满足条件的M点坐标为(1,3)或( ,
, )
)
分析:(1)利用圆的切线的性质,结合勾股定理,可求r的值;
(2)设出直线方程,利用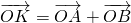 ,表示出
,表示出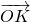 ,求出模长,利用基本不等式即可求得结论.
,求出模长,利用基本不等式即可求得结论.
(3)由题意画出过N作圆的切线,NT的中点就是所求M,求出切点坐标即可取得M点的坐标.
点评:本题考查圆的切线的性质,考查向量知识的运用,两直线垂直的性质,点到直线的距离公式应用,以及求两直线的交点坐标的方法.
∵过点Q(-2,
 ) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4
) 作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4∴r=OD=
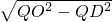 =
=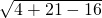 =3;
=3;(2)设直线l的方程为
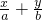 =1(a>0,b>0),即bx+ay-ab=0,则A(a,0),B(0,b),
=1(a>0,b>0),即bx+ay-ab=0,则A(a,0),B(0,b),
∵
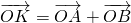 ,∴
,∴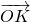 =(a,b),∴|
=(a,b),∴|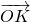 |=
|=
∵直线l与圆C相切,∴
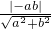 =3
=3∴3
 =ab≤
=ab≤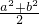
∴a2+b2≥36
∴|
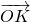 |≥6
|≥6当且仅当a=b=3
 时,|
时,|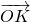 |的最小值为6.
|的最小值为6.(3)∵切线MN⊥OT,∴|MT|2=|MO|2-9,又|MN|=|MT|,∴|MN|2=|MO|2-9,
M(x1,y1),过N(2,3)的直线的斜率为k,所以NT的方程为:y-3=k(x-2),
与圆的方程x2+y2=9联立,
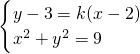 ,消去y可得:(k2+1)x2+2(3-2k)kx+4k2-12k=0,
,消去y可得:(k2+1)x2+2(3-2k)kx+4k2-12k=0,因为直线与圆相切,所以△=0,即[2(3-2k)k]2-4(k2+1)(4k2-12k)=0,
化简得:5k2+12k=0,解得k=0或k=-
 ,
,当k=0时,x=0,此时T(0,3),当k=
 时,x=
时,x= ,此时T(
,此时T( ,
, )
)∴满足条件的M点坐标为(1,3)或(
 ,
, )
)分析:(1)利用圆的切线的性质,结合勾股定理,可求r的值;
(2)设出直线方程,利用
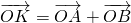 ,表示出
,表示出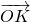 ,求出模长,利用基本不等式即可求得结论.
,求出模长,利用基本不等式即可求得结论.(3)由题意画出过N作圆的切线,NT的中点就是所求M,求出切点坐标即可取得M点的坐标.
点评:本题考查圆的切线的性质,考查向量知识的运用,两直线垂直的性质,点到直线的距离公式应用,以及求两直线的交点坐标的方法.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 作圆C:x2+y2=r2(
作圆C:x2+y2=r2( )的切线,切点为D,且QD=4.
)的切线,切点为D,且QD=4. ,求
,求 的最小值(O为坐标原点).
的最小值(O为坐标原点). 作圆C:x2+y2=r2(
作圆C:x2+y2=r2( )的切线,切点为D,且QD=4.
)的切线,切点为D,且QD=4. ,求
,求 的最小值(O为坐标原点).
的最小值(O为坐标原点). 作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.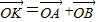 ,求
,求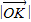 的最小值(O为坐标原点).
的最小值(O为坐标原点).