题目内容
若直线
始终平分圆
的周长，则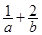
的最小值为
| A．1 | B．5 | C．3＋ | D． |
D
解析试题分析：因为根据题意可知，直线始终平分圆的周长，则说明圆的标准方程为
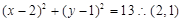是圆心坐标，那么直线过圆心，则有2a+2b-2=0,a+b=1,那么
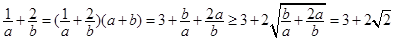，当且仅当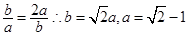
时成立，故选D.
考点：本试题主要是考查了直线与圆的位置关系的运用。
点评：解决该试题的关键是理解，直线平分圆的周长意味着，直线过圆心，这是一个重要的结论，要理解。同时能利用不等式的思想来求解最值，注意一正二定三相等的运用。
练习册系列答案
相关题目
已知圆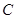
与直线
都相切，圆心在直线
上，则圆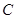的方程为（ ）
A． | B． |
C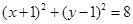． | D． |
若直线3x＋y＋a＝0过圆x2＋y2＋2x－4y＝0的圆心，则a的值为( )
| A．－1 | B．1 | C．3 | D．－3 |
已知圆
,
过点
的直线,则（ ）
A．与 相交 | B．与相切 |
| C．与相离 | D．以上三个选项均有可能 |
已知圆
，圆
，则两圆公切线的条数有( )
A． 条 | B． 条 | C． 条 | D． 条 |
与圆
交于M,N两点，且M,N关于直线
对称，动点P(a，b)在不等式组
表示的平面区域内部及边界上运动，则
取值范围是（ ）
若直线3x＋y＋a＝0过圆x2＋y2＋2x－4y＝0的圆心，则a的值为( )．
| A．－1 | B．1 | C．3 | D．－3 |
若圆C：x2＋y2＋2x－4y＋3＝0关于直线2ax＋by＋6＝0对称，则由点(a,b)向圆所作的切线长的最小值是
| A．2 | B．3 | C．4 | D．6 |
当圆
的面积最大时,圆心坐标是 ( )
A． | B． | C． | D． |