题目内容
8.对一切实数x,函数f(x)满足:xf(x)=2f(1-x)+1,则f(5)=$\frac{1}{12}$.分析 根据所给条件,构造另一方程,利用方程组法求解函数的解析式.然后代入求解即可.
解答 解:∵2f(1-x)+1=xf(x) ①,
用x代替1-x得:2f(x)+1=(1-x)f(1-x) ②
(1)若x=1.在①中取x=0,得:f(1)=-$\frac{1}{2}$.即当x=1时,f(x)=-$\frac{1}{2}$,
(2)若x≠1.①×(1-x)得:2(1-x)f(1-x)+(1-x)=x(1-x)f(x) ③
②×2得:4f(x)+2=2(1-x)f(1-x) ④
③+④,消去f(1-x),得:f(x)=$\frac{x-3}{{x}^{2}-x+4}$,(x≠1)而当x=1时,也满足f(x)=$\frac{x-3}{{x}^{2}-x+4}$,
综上,对任意x∈R,f(x)=$\frac{x-3}{{x}^{2}-x+4}$,
则f(5)=$\frac{5-3}{25-5+4}$=$\frac{2}{24}$=$\frac{1}{12}$,
故答案为:$\frac{1}{12}$.
点评 本题主要考查函数值的计算,利用抽象函数的关系,利用方程组法求出函数f(x)的表达式是解决本题的关键.

练习册系列答案
相关题目
18.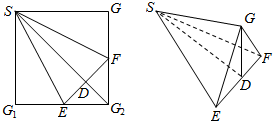 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )
 如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )
如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3中点,D是EF与SG2的交点,现沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体G-SEF中必有( )| A. | SD⊥平面EFG | B. | SE⊥GF | C. | EF⊥平面SEG | D. | SE⊥SF |
19.方程x3-2=0的根所在的区间是( )
| A. | (-2,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
3.在△ABC中,角A,B,C所对的边分别为a,b,c,且(a+b+c)(b+c-a)=bc,则A=( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
13.执行如图所示的程序框图,ze输出S的值为( )


| A. | 10 | B. | -6 | C. | 3 | D. | 12 |