题目内容

若
a
=(2-x，x-1)，
b
=(1，
2-x
x
)，则使不等式
a
•
b
＞0成立的x的取值范围是
 
．
分析：根据所给的向量坐标，写出两个向量的数量积，使得数量积大于零，解关于变量x的不等式，本题出现的是一个分式不等式，解题时先要通分，再把商的形式变化为乘积形式，用穿根法写出不等式的解．
解答：解：∵
a
=(2-x，x-1)，
b
=(1，
2-x
x
)，
a
•
b
＞0，
∴2-x+（x-1）
2-x
x
＞0，
∴
(x-2)(2x-1)
x
＜ 0
∴x（x-2）（2x-1）＜0，
用穿根法写出不等式的解，
x＜0或
1
2
＜ x＜2，
故答案为：（-∞，0）∪（
1
2
，2）
点评：两个向量的数量积是一个数量，它的值是两个向量的模与两向量夹角余弦的乘积，结果可正、可负、可以为零，其符号由夹角的余弦值确定．
练习册系列答案
相关题目
对于定义在D上的函数y=f（x），若同时满足．
①存在闭区间[a，b]⊆D，使得任取x1∈[a，b]，都有f（x1）=c （c是常数）；
②对于D内任意x2，当x2∉[a，b]时总有f（x2）＞c称f（x）为“平底型”函数．
（1）（理）判断f1（x）=|x-1|+|x-2|，f2（x）=x+|x-2|是否是“平底型”函数？简要说明理由；
（文）判断f1（x）=|x-1|+|x-2|，f2（x）=x-|x-3|是否是“平底型”函数？简要说明理由；
（2）（理）设f（x）是（1）中的“平底型”函数，若|t-k|+|t+k|≥|k|•f（x），k∈R且k≠0，对一切t∈R恒成立，求实数x的范围；
（文）设f（x）是（1）中的“平底型”函数，若|t-1|+|t+1|≥f（x），对一切t∈R恒成立，求实数x的范围；
（3）（理）若F（x）=mx+
x2+2x+n
，x∈[-2，+∞）是“平底型”函数，求m和n的值；
（文）若F（x）=m|x-1|+n|x-2|是“平底型”函数，求m和n满足的条件．
已知函数f（x）的图象在[a，b]上连续不断，定义：f1（x）=min{f（t）|a≤t≤x}（x∈[a，b]），f2（x）=max{f（t）|a≤t≤x}（x∈[a，b]）．其中，min{f（x）|x∈D}表示函数f（x）在D上的最小值，max{f（x）|x∈D}表示函数f（x）在D上的最大值．若存在最小正整数k，使得f2（x）-f1（x）≤k（x-a）对任意的x∈[a，b]成立，则称函数f（x）为[a，b]上的“k阶收缩函数”．
（1）若f（x）=cosx，x∈[0，π]，试写出f1（x），f2（x）的表达式；
（2）已知函数f（x）=x2，x∈[-1，4]，试判断f（x）是否为[-1，4]上的“k阶收缩函数”，如果是，求出对应的k；如果不是，请说明理由；
（3）已知b＞0，函数f（x）=-x3+3x2是[0，b]上的2阶收缩函数，求b的取值范围．
已知函数f（x）是区间D⊆[0，+∞）上的增函数．若f（x）可表示为f（x）=f1（x）+f2（x），其中f1（x）是D上的增函数，f2（x）是D上的减函数，且函数f2（x）的值域A⊆[0，+∞），则称函数f（x）的区间D上的“偏增函数”
（1）试说明y=sinx+cosx是区间（0，
π
4
）上的“偏增函数”；
（2）记f1（x）=x，f2（x）=
a
x
（a为常数），是判断f（x）=f1（x）+f2（x）是否是区间（0，1]上的“偏增函数”，若是，证明你的结论，若不是，请说明理由．
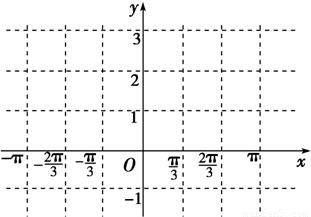
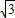已知a=2（cosωx，cosωx），b=（cosωx，sinωx）（其中0＜ω＜1），函数f（x）=a•b，若直线x=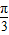是函数f（x）图象的一条对称轴，
（1）试求ω的值；
（2）先列表再作出函数f（x）在区间[-π，π]上的图象．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网