题目内容
设向量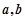 满足
满足
(1)求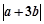 的值;
的值;
(2)求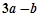 与
与 夹角的正弦值.
夹角的正弦值.
(1)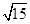 ;(2)
;(2) .
.
解析试题分析:(1)要求模先平方, 得
得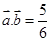 ,只需将
,只需将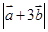 ;(2)求向量夹角采用公式
;(2)求向量夹角采用公式 .
.
试题解析:⑴由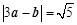 ,得
,得 ,所以
,所以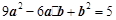 , 2分
, 2分
因为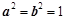 ,所以
,所以 . 4分
. 4分
因此 ,所以
,所以 . 8分
. 8分
⑵设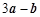 与
与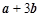 的夹角为
的夹角为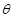 ,
,
因为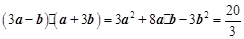 , 10分
, 10分
则 , 12分
, 12分
因为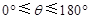 ,所以
,所以 ,
,
所以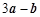 与
与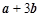 的夹角的正弦值为
的夹角的正弦值为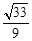 . 14分
. 14分
考点:向量的模及夹角.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
若向量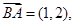
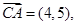 则
则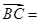 ( )
( )
A.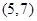 | B.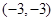 | C.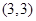 | D.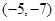 |
若平面向量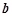 与
与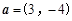 的夹角是
的夹角是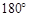 ,且
,且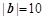 ,则
,则 ( ).
( ).
A.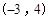 | B.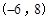 |
C.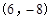 | D.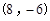 |
设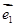 与
与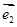 是不共线向量,
是不共线向量,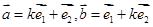 ,若
,若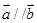 且
且 ,则实数
,则实数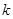 的值为( )
的值为( )
| A.0 | B.1 | C.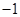 | D.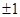 |
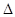 OAB中,点A是BC的中点,点D是将向量
OAB中,点A是BC的中点,点D是将向量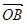 分为2:1的一个分点,DC和OA交于点E.设
分为2:1的一个分点,DC和OA交于点E.设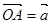 ,
,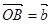
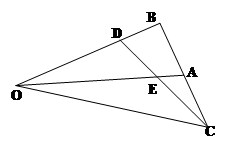
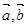 表示
表示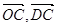 ;
;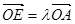 ,求实数
,求实数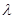 的值.
的值.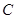 在
在 的边
的边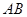 所在的直线上,
所在的直线上,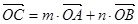 ,求证:
,求证: .
.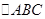 中,
中,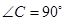 ,点E是BC上一点,且满足:
,点E是BC上一点,且满足: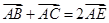 ,以A为圆心,AC的长为半径作圆交AB于D,交AE于F.若
,以A为圆心,AC的长为半径作圆交AB于D,交AE于F.若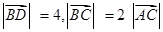 ,求
,求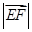 的值.
的值. 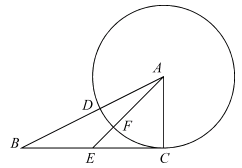
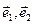 为不共线向量
为不共线向量 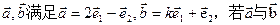
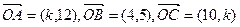 ,且A、B、C三点共线,则
,且A、B、C三点共线,则