Question

【题目】已知f(x)是定义在[－1,1]上的奇函数，且f(1)＝1，若a，b∈[－1,1]，a＋b≠0时

成立．

(Ⅰ)判断f(x)在[－1,1]上的单调性，并证明；

(Ⅱ)解不等式：；

(Ⅲ)若f(x)≤m2－2am＋1对所有的a∈[－1,1]恒成立，求实数m的取值范围

Answer 1

【答案】(Ⅰ) 单调递增(Ⅱ) (Ⅲ) m＝0 或m≤－2或m≥2

【解析】

试题分析：（Ⅰ）任取x1，x2∈[-1，1]，且x1＜x2，利用函数的单调性的定义证明f（x）在[-1，1]上单调递增；（Ⅱ）利用f（x）在[-1，1]上单调递增，列出不等式组，即可求出不等式的解集；（Ⅲ）问题转化为m2-2am≥0，对a∈[-1，1]恒成立，通过①若m=0，②若m≠0，分类讨论，判断求解即可

试题解析：(Ⅰ)任取x1，x2∈[－1,1]，且x1<x2，则－x2∈[－1,1]，∵f(x)为奇函数，

∴f(x1)－f(x2)＝f(x1)＋f(－x2)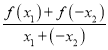＝·(x1－x2)，2分

由已知得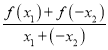>0，x1－x2<0，∴f(x1)－f(x2)<0，即f(x1)<f(x2)．

∴f(x)在[－1,1]上单调递增． 4分

(Ⅱ)∵f(x)在[－1,1]上单调递增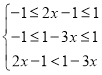，∴6分

∴不等式的解集为. 7分

(Ⅲ)∵f(1)＝1，f(x)在[－1,1]上单调递增．∴在[－1,1]上，f(x)≤1.

问题转化为m2－2am＋1≥1，即m2－2am≥0，对a∈[－1,1]恒成立． 9分

下面来求m的取值范围．设g(a)＝－2m·a＋m2≥0.

①若m＝0，则g(a)＝0≥0，对a∈[－1,1]恒成立．

②若m≠0，则g(a)为a的一次函数，若g(a)≥0，对a∈[－1，1]恒成立，

必须g(－1)≥0且g(1)≥0，∴m≤－2或m≥2.

综上，m＝0 或m≤－2或m≥2 12