题目内容
 如图所示,在正三棱柱ABC-A1B1C1中,D是AC的中点,AA1:AB=
如图所示,在正三棱柱ABC-A1B1C1中,D是AC的中点,AA1:AB=| 2 |
分析:要求两条异面直线所成的角,需要通过见中点找中点的方法,找出边的中点,连接出中位线,得到平行,从而得到两条异面直线所成的角,得到角以后,再在三角形中求出角,利用余弦定理得到角的余弦值,得到角的大小.
解答:解:取A1C1的中点D1,连接B1D1,
∵D是AC的中点,
∴B1D1∥BD,
∴∠AB1D1即为异面直线AB1与BD所成的角.
连接AD1,设AB=a,则AA1=
a,
∴AB1=
a,B1D1=
a,AD1=
=
a.
∴cos∠AB1D1=
=
,
∴∠AB1D1=60°.
故答案为:60°
∵D是AC的中点,
∴B1D1∥BD,
∴∠AB1D1即为异面直线AB1与BD所成的角.
连接AD1,设AB=a,则AA1=
| 2 |
∴AB1=
| 3 |
| ||
| 2 |
|
| 3 |
| 2 |
∴cos∠AB1D1=
3a2+
| ||||||
2×
|
| 1 |
| 2 |
∴∠AB1D1=60°.
故答案为:60°
点评:本题考查异面直线所成的角,本题是一个典型的异面直线所成的角的问题,解答时也是应用典型的见中点找中点的方法,注意求角的三个环节,一画,二证,三求.

练习册系列答案
相关题目
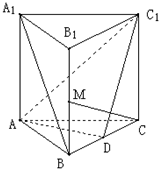 如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M 是棱BB1的中点,又CM⊥AC1,
如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M 是棱BB1的中点,又CM⊥AC1,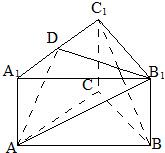 如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为
如图所示,在正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为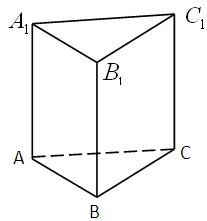
 如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M在棱BB1上,且BM=
如图所示,在正三棱柱ABC-A1B1C1中,底面边长是2,D是棱BC的中点,点M在棱BB1上,且BM= (2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.
(2012•日照一模)如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点.