题目内容
函数 在
在 上是减函数,在
上是减函数,在 上是增函数;函数
上是增函数;函数 在
在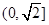 上是减函数,在
上是减函数,在 上是增函数;函数
上是增函数;函数 在
在 上是减函数,在
上是减函数,在 上是增函数;……利用上述所提供的信息解决问题:若函数
上是增函数;……利用上述所提供的信息解决问题:若函数 的值域是
的值域是 ,则实数
,则实数 的值是 .
的值是 .
 在
在 上是减函数,在
上是减函数,在 上是增函数;函数
上是增函数;函数 在
在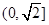 上是减函数,在
上是减函数,在 上是增函数;函数
上是增函数;函数 在
在 上是减函数,在
上是减函数,在 上是增函数;……利用上述所提供的信息解决问题:若函数
上是增函数;……利用上述所提供的信息解决问题:若函数 的值域是
的值域是 ,则实数
,则实数 的值是 .
的值是 .2
根据一系列函数的性质进行归纳和类比,总结出函数y=x+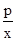 (p为常数)的性质和增减区间,从而求解.
(p为常数)的性质和增减区间,从而求解.
解答:解:∵函数y=x+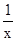 在(0,1]上是减函数,在[1,+∞)上是增函数;
在(0,1]上是减函数,在[1,+∞)上是增函数;
函数y=x+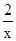 在(0,
在(0,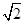 ]上是减函数,在[
]上是减函数,在[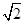 ,+∞)上是增函数;
,+∞)上是增函数;
函数y=x+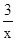 在(0,
在(0,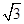 ]上是减函数,在[
]上是减函数,在[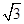 ,+∞)上是增函数;
,+∞)上是增函数;
∴函数y=x+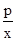 (p为正常数)在(0,
(p为正常数)在(0,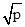 ]上是减函数,在[
]上是减函数,在[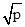 ,+∞)上是增函数;
,+∞)上是增函数;
∵函数y="x+"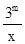 (x>0)的值域是[6,+∞),
(x>0)的值域是[6,+∞),
∴函数在x=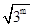 取得最小值为6,
取得最小值为6,
∴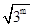 +
+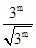 =6,
=6,
解得m=2,故答案为2.
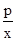 (p为常数)的性质和增减区间,从而求解.
(p为常数)的性质和增减区间,从而求解.解答:解:∵函数y=x+
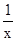 在(0,1]上是减函数,在[1,+∞)上是增函数;
在(0,1]上是减函数,在[1,+∞)上是增函数;函数y=x+
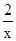 在(0,
在(0,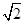 ]上是减函数,在[
]上是减函数,在[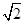 ,+∞)上是增函数;
,+∞)上是增函数;函数y=x+
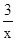 在(0,
在(0,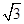 ]上是减函数,在[
]上是减函数,在[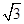 ,+∞)上是增函数;
,+∞)上是增函数;∴函数y=x+
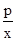 (p为正常数)在(0,
(p为正常数)在(0,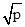 ]上是减函数,在[
]上是减函数,在[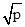 ,+∞)上是增函数;
,+∞)上是增函数;∵函数y="x+"
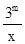 (x>0)的值域是[6,+∞),
(x>0)的值域是[6,+∞),∴函数在x=
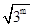 取得最小值为6,
取得最小值为6,∴
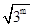 +
+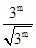 =6,
=6,解得m=2,故答案为2.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 的图象关于点(-
的图象关于点(- ,0)对称,且满足
,0)对称,且满足 ,
, ,
, ,则
,则 的值是
的值是 万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值
万元的一条流水线,要提高该流水线的生产能力,就要对其进行技术改造,从而提高产品附加值,改造需要投入,假设附加值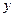 万元与技术改造投入
万元与技术改造投入 万元之间的关系满足:①
万元之间的关系满足:① 和
和 时,
时, ;③
;③ ,其中
,其中 为常数,且
为常数,且 .
. ,求
,求 表达式,并求
表达式,并求 出附加值
出附加值 的方程
的方程 有一个负根,但没有正根,则实数
有一个负根,但没有正根,则实数 的取值范围是
的取值范围是  元,并且每件产品需向总公司交
元,并且每件产品需向总公司交 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件. (万元)与每件产品的售价
(万元)与每件产品的售价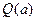 .
.
 的零点个数为 ( )
的零点个数为 ( )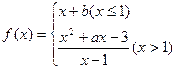 在
在 处连续,则
处连续,则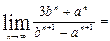 ( )
( ) ”如下:
”如下: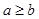 时,
时, 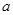
 =
=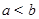 时,
时,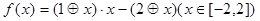 的最大值等于( )
的最大值等于( )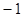
 已知函数
已知函数 ,则
,则 的值为
的值为