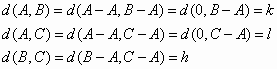Question

已知集合S_n＝{X|X＝(x₁，x₂，…，x_n)，x₁∈{0，1}，i＝{1，2，…，n}(n≥2)对于A＝(a₁，a₂，…a_n)，B＝(b₁，b₂，…b_n)∈S_n，定义A与B的差为A－B＝(|a₁－b₁|，|a₂－b₂||，…|a_n－b_n|)；A与B之间的距离为d(A，B)＝|a₁－b₁|

(Ⅰ)当n＝5时，设A＝(0，1，0，0，1)，B＝(1，1，1，0，0)，求A－B，d(A，B)；

(Ⅱ)证明：A，B，C∈S_n，有A－B∈S_n，且d(A－C，B－C)＝d(A，B)；

(Ⅲ)证明：A，B，C∈S_n，d(A，B)，d(A，C)，d(B，C)三个数中至少有一个是偶数

Answer 1

答案：
解析：

(Ⅰ)解：＝(1，0，1，0，1) 　　＝3 　　(Ⅱ)证明：设 　　因为，所以 　　从而 　　由题意知 　　当时， 　　当时， 　　所以 　　(Ⅲ)证明：设 　　 　　记由(Ⅱ)可知 　　 　　所以中1的个数为k，中1的个数为 　　设是使成立的的个数．则 　　由此可知，三个数不可能都是奇数 　　即三个数中至少有一个是偶数．