题目内容
设函数 ,
, . 若当
. 若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( ).
的取值范围是( ).
A. B.
B. C.
C. D.
D.
【答案】
A
【解析】
试题分析:∵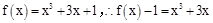 。
。
设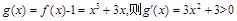 ,
,
所以g(x)是递增的奇函数。
由f(msinθ)+f(1-m)>2,
∴f(msinθ)-1>1-f(1-m),即g(msinθ)>g(m-1)
∴msinθ>m-1,∴1>m(1-sinθ)。
因为0<θ<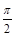 时,
时,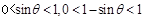 ,
, >1,而m<
>1,而m< ,
,
∴m 1.故选A。
1.故选A。
考点:本题主要考查函数的奇偶性、单调性,利用导数研究函数的单调性,恒成立问题解法。
点评:中档题,抽象不等式问题,武威要利用函数的奇偶性、单调性,转化成具体不等式。恒成立问题,往往要通过“分离参数法”转化成求函数的最值问题。本题比较典型。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 .
. 时
时 取得极值,求a的值,并讨论
取得极值,求a的值,并讨论 .
. 。(Ⅰ)若函数
。(Ⅰ)若函数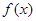 在
在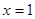 处与直线
处与直线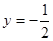 相切,①求实数
相切,①求实数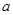 ,b的值;②求函数
,b的值;②求函数 上的最大值;(Ⅱ)当
上的最大值;(Ⅱ)当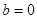 时,若不等式
时,若不等式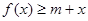 对所有的
对所有的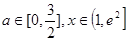 都成立,求实数m的取值范围。
都成立,求实数m的取值范围。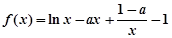 .
.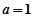 时,过原点的直线与函数
时,过原点的直线与函数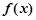 的图象相切于点P,求点P的坐标;
的图象相切于点P,求点P的坐标;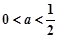 时,求函数
时,求函数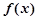 的单调区间;
的单调区间;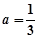 时,设函数
时,设函数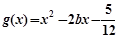 ,若对于
,若对于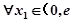 ],
],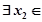 [0,1]
[0,1]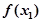 ≥
≥ 成立,求实数b的取值范围.(
成立,求实数b的取值范围.(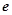 是自然对数的底,
是自然对数的底,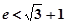 )。
)。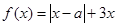 ,其中
,其中 .
. 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为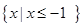 ,求a的值.
,求a的值.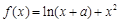 .
.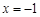 时
时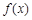 取得极值,求a的值,并讨论
取得极值,求a的值,并讨论 .
.