题目内容
10.已知数列{an}满足a1=b(b>0),an+1(an+1)=-1(n∈N*),则使得an=b的n的值可以为( )| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
分析 a1=b(b>0),an+1(an+1)=-1(n∈N*),可得${a}_{2}=\frac{-1}{b+1}$,a3=-$\frac{1+b}{b}$,b4=b,…,可得an+3=an.即可得出.
解答 解:∵a1=b(b>0),an+1(an+1)=-1(n∈N*),
∴${a}_{2}=\frac{-1}{b+1}$,a3=$\frac{-1}{1-\frac{1}{1+b}}$=-$\frac{1+b}{b}$,b4=$\frac{-1}{1-\frac{1+b}{b}}$=b,…,
可得an+3=an.
∴a16=a3×5+1=a1=b.
∴使得an=b的n的值可以为16.
故选:C.
点评 本题考查了递推关系的应用、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.函数f(x)=sinx•ln|x|的图象大致是( )
| A. |  | B. |  | C. | 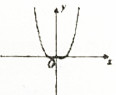 | D. |  |
6.写有1,2,3,4,5的五张卡片,每次从中随机抽取一张(不放回).连续抽取三次,其中第二次恰好抽到奇数数字,且三次不全是奇数数字的不同取法有( )
| A. | 24种 | B. | 30种 | C. | 36种 | D. | 34种 |
 ,
, ,
, .若
.若 ,则实数
,则实数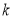 的值等于 .
的值等于 .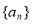 的前
的前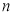 项和记为
项和记为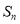 ,
, ,
,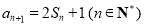 .
.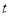 为何值时,数列
为何值时,数列 的前
的前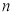 项和
项和 有最大值,且
有最大值,且 ,
,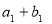 ,
, ,
,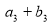 成等比数列,求
成等比数列,求 .
.