题目内容
（）（本小题满分12分）
设函数
,其中常数
(Ⅰ)讨论
的单调性;
(Ⅱ)若当x≥0时，>0恒成立，求
的取值范围.
：（I）
由
知，当
时，
，故
在区间
是增函数；
当
时，
，故在区间
是减函数；
当
时，，故在区间
是增函数.
综上，当时，在区间和是增函数，在区间是减函数.
（II）由（I）知，当
时，在
或
处取得最小值.
由假设知
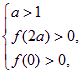即
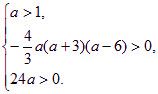解得 
故
的取值范围是（1，6）w.w.w.k.s.5.u.c.o.m 
解析:
：因为第(Ⅰ)题中要求函数的单调区间,利用导数的正负即可求出,所以首先要求出函数的导数,然后解不等式和即可. 第(Ⅱ)小题是一个恒成立问题,转化为求函数的最值解决,所以要求出函数在x≥0时的最小值.
练习册系列答案
相关题目
的一元二次函数
（Ⅰ）设集合P={1，2， 3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为
和
，求函数
在区间[
上是增函数的概率；（Ⅱ）设点（
内的随机点，求函数
上是增函数的概率。
，且
。①求
的最大值及最小值；②求
的三视图如图所示，
,A1A=
,AB=
,AC=2,A1C1=1,
在线段
上且
=
.
⊥平面
；
的余弦值.