题目内容

P是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)上异于顶点的任意一点，F1，F2为其左、右焦点，则以PF2为直径的圆与以长轴为直径的圆的位置是（　　）
分析：画出图形，利用三角形的中位线与椭圆的定义，推出两个圆的圆心距与半径关系，推出结果．
解答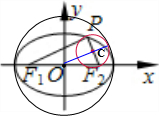：解：如图：因为P是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)上异于顶点的任意一点，F1，F2为其左、右焦点，则以PF2为直径的圆的半径是
1
2
|PF2|，以长轴为直径的圆的半径为a，
OC
∥
.
1
2
PF1．圆心距|OC|=
1
2
PF1，因为|OC|+
1
2
|PF2|=a，所以两个圆相内切
故选B．
点评：本题考查椭圆的基本性质，椭圆的定义的应用，考查计算能力．
练习册系列答案
相关题目
精英家教网给定椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），称圆心在坐标原点O，半径为
a2+b2
的圆是椭圆C的“伴随圆”．
（1）若椭圆C过点(
5
，0)，且焦距为4，求“伴随圆”的方程；
（2）如果直线x+y=3
2
与椭圆C的“伴随圆”有且只有一个交点，那么请你画出动点Q（a，b）轨迹的大致图形；
（3）已知椭圆C的两个焦点分别是F1（-
2
，0）、F2（
2
，0），椭圆C上一动点M1满足|
M1F1
|+|
M1F
2|=2
3
．设点P是椭圆C的“伴随圆”上的动点，过点P作直线l1、l2使得l1、l2与椭圆C都各只有一个交点，且l1、l2分别交其“伴随圆”于点M、N．当P为“伴随圆”与y轴正半轴的交点时，求l1与l2的方程，并求线段|
MN
|的长度．
已知F1、F2是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，点P(-1，
2
2
)在椭圆上，线段PF2与y轴的交点M满足
PM
=
MF2
．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）过F2作不与x轴重合的直线l，l与圆x2+y2=a2+b2相交于A、B并与椭圆相交于C、D，当
F1A
•
F1B
=λ，且λ∈[
2
3
，1]时，求△F1CD的面积S的取值范围．
设 P（x，y），Q（x′，y′） 是椭圆 
x2
a2
+
y2
b2
=1（a＞0，b＞0）上的两点，则下列四个结论：①a2+b2≥（x+y）2；②
1
x2
+
1
y2
≥(
1
a
+
1
b
)2；③
a2
x2
+
b2
y2
≥4；④
xx′
a2
+
yy′
b2
≤1．其中正确的个数为（　　）
（2009•河东区二模）已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)．
（1）设F是椭圆的一个焦点，M椭圆上的任意一点，|MF|的最大值与最小值的算术平均等于4，椭圆的顶点A与N（-2，0）关于直线x+y=0对称，求此椭圆方程；
（2）设点P是椭圆
x2
a2
+
y2
b2
=1上异于长轴端点的任意一点，F1、F2为两焦点，记∠F1PF2=θ，求证|PF1|•|PF2|=
2b2
1+cosθ
．
（2013•静安区一模）已知椭圆
x2
a2
+
y2
b2
=1的两个焦点为F1（-c，0）、F2（c，0），c2是a2与b2的等差中项，其中a、b、c都是正数，过点A（0，-b）和B（a，0）的直线与原点的距离为
3
2
．
（1）求椭圆的方程；
（2）点P是椭圆上一动点，定点A1（0，2），求△F1PA1面积的最大值；
（3）已知定点E（-1，0），直线y=kx+t与椭圆交于C、D相异两点．证明：对任意的t＞0，都存在实数k，使得以线段CD为直径的圆过E点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网