题目内容
(本小题满分7分)选修4—5:不等式选将
已知定义在R上的函数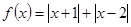 的最小值为
的最小值为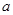 .
.
(I)求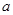 的值;
的值;
(II)若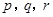 为正实数,且
为正实数,且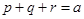 ,求证:
,求证: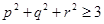 .
.
已知定义在R上的函数
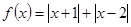 的最小值为
的最小值为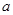 .
.(I)求
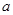 的值;
的值;(II)若
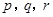 为正实数,且
为正实数,且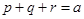 ,求证:
,求证: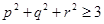 .
.(I)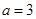 ;(II)参考解析
;(II)参考解析
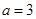 ;(II)参考解析
;(II)参考解析试题分析:(I)已知定义在R上的函数
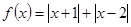 的最小值,由绝对值的性质可得函数的最小值.即可得到结论.
的最小值,由绝对值的性质可得函数的最小值.即可得到结论.(II)由(I)可得
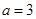 ,再根据柯西不等式即可得到结论.
,再根据柯西不等式即可得到结论.试题解析:(I)因为
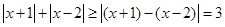 ,当且仅当
,当且仅当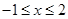 时,等号成立,所以
时,等号成立,所以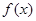 的最小值等于3,即
的最小值等于3,即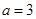 .
.(II)由(I)知
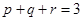 ,又因为
,又因为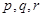 是正数,所以
是正数,所以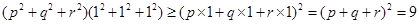 ,即
,即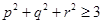 .
.
练习册系列答案
相关题目
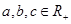 ,且
,且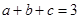 ,
,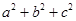 的最小值为
的最小值为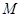 .
.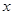 的不等式
的不等式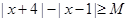 .
.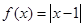 .
. 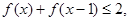 ;
; 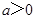 ,求证:
,求证: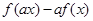 ≤
≤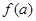 .
. 的解集为( )
的解集为( )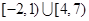



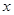 的方程
的方程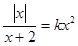 有四个不同的实数解,则实数
有四个不同的实数解,则实数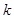 的取值范围为()
的取值范围为() 


