题目内容
14.比较大小:sin1和sin1.5
cos1和cos1.5
tan3和tan2.
分析 利用正弦函数、余弦函数、正切函数的单调性,推出结果即可.
解答 解:由于1<1.5<$\frac{π}{2}$,y=sinx在x∈(0,$\frac{π}{2}$)是增函数,∴sin1<sin1.5.
y=cosx在x∈(0,$\frac{π}{2}$)是减函数,∴cos1>cos1.5.
$\frac{π}{2}$<2<3<π,
y=tanx在在x∈($\frac{π}{2}$,π)是增函数,∴tan3>tan2.
点评 本题考查正切函数的单调性,正弦函数的单调性,余弦函数的单调性的应用,考查计算能力.

练习册系列答案
相关题目
9.已知$\overrightarrow{a}$=(-2,0,1),$\overrightarrow{b}$=(2,k,3),$\overrightarrow{c}$=(1,-1,2),若$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$三个向量共面,则实数k的值为( )
| A. | -$\frac{8}{5}$ | B. | -$\frac{1}{5}$ | C. | 1 | D. | $\frac{8}{5}$ |
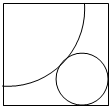 如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.
如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.