题目内容
已知函数f(x)=x2-(2a+1)x+alnx.
(1)当a=1时,求函数f(x)的单调增区间;
(2)求函数f(x)在区间[1,e]上的最小值;
(1)当a=1时,求函数f(x)的单调增区间;
(2)求函数f(x)在区间[1,e]上的最小值;
(1)(0,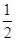 ),(1,+∞) (2)a(lna-a-1)
),(1,+∞) (2)a(lna-a-1)
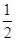 ),(1,+∞) (2)a(lna-a-1)
),(1,+∞) (2)a(lna-a-1)本试题主要考查了导数在研究函数中的运用。
解:(1)当a=1时,f(x)=x2-3x+lnx,定义域为(0,+∞),
f′(x)=2x-3+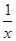 =
=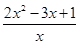 =
=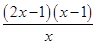 .
.
令f′(x)=0,得x=1或x=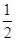 .
.
所以函数f(x)的单调增区间为(0,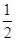 ),(1,+∞).
),(1,+∞).
(2)f′(x)=2x-(2a+1)+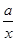 =
=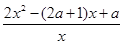 =
=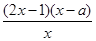 ,令f′(x)=0,得x=a或x=
,令f′(x)=0,得x=a或x=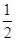 .
.
当a≤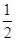 时,f(x)在[
时,f(x)在[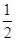 ,+∞)上单调增,所以f(x)在区间[1,e]上单调增;
,+∞)上单调增,所以f(x)在区间[1,e]上单调增;
当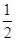 <a≤1时,f(x)在(0,
<a≤1时,f(x)在(0,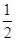 ],[a,+∞)上单调增,所以f(x)在区间[1,e]上单调增.
],[a,+∞)上单调增,所以f(x)在区间[1,e]上单调增.
综上,当a≤1时,f(x)min=f(1)=-2a;
当1<a<e时,
所以f(x)min=f(
解:(1)当a=1时,f(x)=x2-3x+lnx,定义域为(0,+∞),
f′(x)=2x-3+
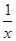 =
=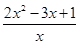 =
=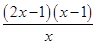 .
.令f′(x)=0,得x=1或x=
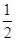 .
.| x | (0,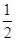 ) ) | 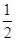 | (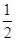 ,1) ,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) |  ? ? | 极大值 | ? | 极小值 | ? |
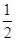 ),(1,+∞).
),(1,+∞). (2)f′(x)=2x-(2a+1)+
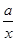 =
=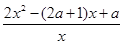 =
=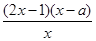 ,令f′(x)=0,得x=a或x=
,令f′(x)=0,得x=a或x=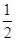 .
.当a≤
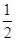 时,f(x)在[
时,f(x)在[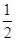 ,+∞)上单调增,所以f(x)在区间[1,e]上单调增;
,+∞)上单调增,所以f(x)在区间[1,e]上单调增;当
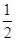 <a≤1时,f(x)在(0,
<a≤1时,f(x)在(0,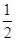 ],[a,+∞)上单调增,所以f(x)在区间[1,e]上单调增.
],[a,+∞)上单调增,所以f(x)在区间[1,e]上单调增.综上,当a≤1时,f(x)min=f(1)=-2a;
当1<a<e时,
| x | (1,a) | a | (a,e) |
| f′(x) | - | 0 | + |
| f(x) | ?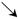 | a(lna-a-1) | ?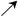 |

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 ,其中
,其中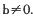
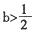 时,判断函数
时,判断函数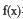 在定义域上的单调性;
在定义域上的单调性;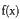 的极值点;
的极值点;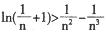 都成立.
都成立.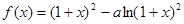 在
在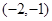 上是增函数,在
上是增函数,在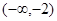 上为减函数.
上为减函数.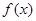 的表达式;
的表达式;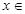
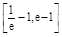 时,不等式
时,不等式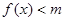 恒成立,求实数
恒成立,求实数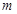 的值;
的值;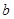 使得关于
使得关于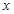 的方程
的方程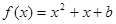 在区间[0,2]上恰好有两个相异的实根,若存在,求实数
在区间[0,2]上恰好有两个相异的实根,若存在,求实数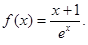
 的单调区间;
的单调区间;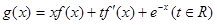 ,是否存在实数a、b、c∈[0,1],使得
,是否存在实数a、b、c∈[0,1],使得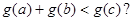 若存在,求出t的取值范围;若不存在,说明理由.
若存在,求出t的取值范围;若不存在,说明理由.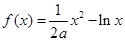 ,其中
,其中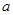 为大于零的常数.
为大于零的常数.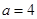 时,求函数
时,求函数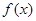 的单调区间和极值;
的单调区间和极值;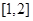 上至少存在一点
上至少存在一点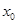 ,使得
,使得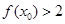 成立,求
成立,求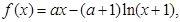 其中
其中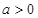 ,
,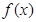 的单调区间;
的单调区间;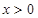 时,证明不等式:
时,证明不等式: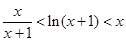 .
.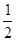 +
+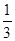 +
+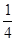 +L
+L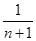 (
( ).
).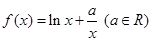
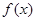 的单调性;
的单调性;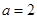 时,求函数
时,求函数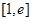 上的最值.
上的最值.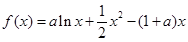 .
.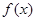 的单调区间;
的单调区间;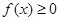 对定义域每的任意
对定义域每的任意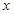 恒成立,求实数
恒成立,求实数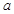 的取值范围;
的取值范围;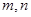 ,不等式
,不等式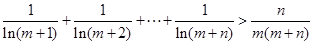 恒成立。
恒成立。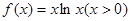 的单调递增区间是
的单调递增区间是