题目内容
甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(Ⅰ)用茎叶图表示这两组数据,并写出乙组数据的中位数;
(Ⅱ)经过计算知甲、乙两人预赛的平均成绩分别为
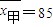 ,
,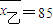 ,甲的方差为 s甲2=35.5;现要从中选派一人参加数学竞赛,你认为选派哪位学生参加较合适?请说明理由;
,甲的方差为 s甲2=35.5;现要从中选派一人参加数学竞赛,你认为选派哪位学生参加较合适?请说明理由;(Ⅲ)若将预赛成绩中的频率视为概率,对甲同学今后3次的数学竞赛成绩进行预测,记这3次成绩中高于80分的次数为ξ,求ξ的分布列及数学期望.
【答案】分析:(I)根据所给的数据,以十位做茎,个位做叶,做出茎叶图,注意图形要做到美观,不要丢失数据.
(II)根据所给的数据做出两个人的平均数和方差,把平均数和方差进行比较,得到两个人的平均数相等,但是乙的方差大于甲的方差,得到要派甲参加.
(III)写出随机变量ξ的可能取值,根据已知判断出ξ~B(3, ),列出随机变量的分布列,利用期望的公式求出期望.
),列出随机变量的分布列,利用期望的公式求出期望.
解答:解:
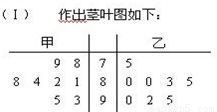
乙组数据的中位数为84
(II)根据所给的数据得
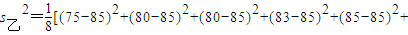
(90-85)2+(92-85)2+(95-85)2]=41
∵ =
=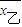 ,s甲2<s乙2,
,s甲2<s乙2,
∴甲的成绩较稳定,派甲参赛比较合适
(III)记“记这3次成绩中高于80分”为事件A,则P(A)= ,
,
随机变量ξ的可能取值为0,1,2,3且ξ~B(3, ),
),
所以P(ξ=k)= ,其中k=0,1,2,3,
,其中k=0,1,2,3,
所以随机变量ξ的分布列为
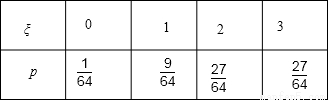
所以Eξ=
点评:对于两组数据,通常要求的是这组数据的方差和平均数,用这两个特征数来表示分别表示两组数据的特征,即平均水平和稳定程度.
(II)根据所给的数据做出两个人的平均数和方差,把平均数和方差进行比较,得到两个人的平均数相等,但是乙的方差大于甲的方差,得到要派甲参加.
(III)写出随机变量ξ的可能取值,根据已知判断出ξ~B(3,
 ),列出随机变量的分布列,利用期望的公式求出期望.
),列出随机变量的分布列,利用期望的公式求出期望.解答:解:

乙组数据的中位数为84
(II)根据所给的数据得
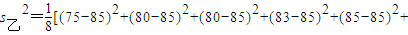
(90-85)2+(92-85)2+(95-85)2]=41
∵
 =
=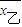 ,s甲2<s乙2,
,s甲2<s乙2,∴甲的成绩较稳定,派甲参赛比较合适
(III)记“记这3次成绩中高于80分”为事件A,则P(A)=
 ,
,随机变量ξ的可能取值为0,1,2,3且ξ~B(3,
 ),
),所以P(ξ=k)=
 ,其中k=0,1,2,3,
,其中k=0,1,2,3,所以随机变量ξ的分布列为

所以Eξ=

点评:对于两组数据,通常要求的是这组数据的方差和平均数,用这两个特征数来表示分别表示两组数据的特征,即平均水平和稳定程度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目