题目内容
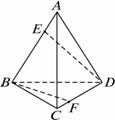
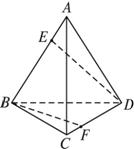
如图,已知正四面体A-BCD的棱长为1,E,F分别为棱AB、CD的中点.
(1)建立适当的空间直角坐标系,写出顶点A,B,C,D的坐标.
(2)求EF的长.
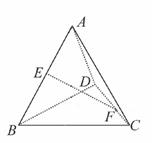
(1)设底面正三角形BCD的中心为点O,连接AO,DO,延长DO交BC于点M,则AO⊥平面BCD,M是BC的中点,且DM⊥BC,过点O作ON∥BC,交CD于点N,则ON⊥DM,故以O为坐标原点,OM,ON,OA所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系![]() .
.
∵正四面体A-BCD的棱长为1,O为底面△BCD的中心.
∴OD=![]() ·DM=
·DM=![]()
![]() =
=![]() ,
,
OM=![]() DM=
DM=![]() .
.
OA=![]() =
=![]() =
=![]() ,
,
∴A(0,0,![]() ),B(
),B(![]() ,-
,-![]() ,0),
,0),![]() C(
C(![]() ,
,![]() ,0),
,0),
D(-![]() ,0,0).
,0,0).
(2)由(1)及中点坐标公式得E(![]() ,-
,-![]() ,
,![]() ),
),
F(-![]() ,
,![]() ,0),
,0),
∴|EF|=![]() =
=![]() .
.

练习册系列答案
相关题目
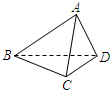 如图,已知正四面体ABCD的棱长为3cm.
如图,已知正四面体ABCD的棱长为3cm.