题目内容
【题目】如图,在四棱锥![]() 中,已知
中,已知![]() 平面
平面![]() ,且四边形
,且四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() .
.
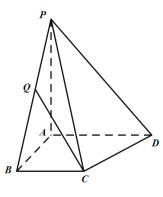
(Ⅰ)求平面![]() 与平面
与平面![]() 所成二面角(锐角)的余弦值;
所成二面角(锐角)的余弦值;
(Ⅱ)点![]() 是线段
是线段![]() 上的动点,当直线
上的动点,当直线![]() 与
与![]() 所成角最小时,求线段
所成角最小时,求线段![]() 的长度.
的长度.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系.利用平面
轴,建立空间直角坐标系.利用平面![]() 和平面
和平面![]() 的法向量,计算出平面
的法向量,计算出平面![]() 与平面
与平面![]() 所成二面角(锐角)的余弦值.
所成二面角(锐角)的余弦值.
(Ⅱ)利用向量共线得到![]() 的坐标.利用向量法求得直线
的坐标.利用向量法求得直线![]() 与
与![]() 所成角为
所成角为![]() 的余弦值
的余弦值![]() 的平方
的平方![]() 的表达式,还原后利用配方法求得
的表达式,还原后利用配方法求得![]() 的最大值,即求得
的最大值,即求得![]() 的最大值,根据余弦函数的单调性可知,此时直线
的最大值,根据余弦函数的单调性可知,此时直线![]() 与
与![]() 所成角最小.根据最值成立的条件,求得线段
所成角最小.根据最值成立的条件,求得线段![]() 的长度.
的长度.
(Ⅰ)分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
取平面![]() 的法向量
的法向量![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,
,![]() ,即
,即![]() ,解得
,解得![]() ,取
,取![]() ,则
,则![]() .
.
设平面![]() 与平面
与平面![]() 所成二面角(锐角)为
所成二面角(锐角)为![]() ,
,
则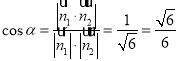 .
.
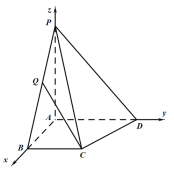
(Ⅱ)设![]() (其中
(其中![]() ),
),
![]() ,设当直线
,设当直线![]() 与
与![]() 所成角为
所成角为![]() ,则
,则![]() ,
,
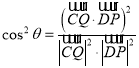
 ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
则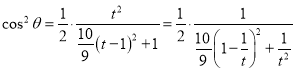
 ,
,
当![]() ,即
,即![]() ,
,![]() 时,
时,![]() 取得最大值,最大值为
取得最大值,最大值为![]() ,此时
,此时![]() 取得最大值.
取得最大值.
由余弦函数单调性可知,此时锐角![]() 取得最小值,且
取得最小值,且![]() .
.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
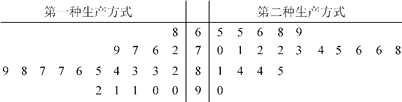
(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|
【题目】已知某产品的销售额![]() 与广告费用
与广告费用![]() 之间的关系如下表:
之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根据表中的数据用最小二乘法求得![]() 对
对![]() 的回归直线方程为
的回归直线方程为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.产品的销售额与广告费用成正相关
B.该回归直线过点![]()
C.当广告费用为10万元时,销售额一定为74万元
D.![]() 的值是20
的值是20
