Question

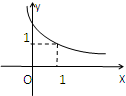函数y=f（x-1）的图象如图所示，它在R上单调递减，现有如下结论：
（1）f（0）＞1；（2）f(

1

2

)＜1；（3）f^-1（1）=0；（4）f-1(

1

2

)＞0．  
其中正确的命题序号为

（2），（3），（4）

．（写出所有正确命题序号）

Answer 1

分析：根据函数图象过点（1，1），点适合解析式，可判定（1）的真假，令x=

3

2

，根据图象可知f（

1

2

）的大小，从而判定（2）的真假，根据原函数与反函数的关系可判定（3）的真假，根据原函数在R上单调递减，则反函数在R上单调递减，可判定（4）的真假．

解答：解：根据函数图象过点（1，1），则f（1-1）=f（0）=1，故（1）不正确；
令x=

3

2

，则f（

3

2

-1）=f（

1

2

），根据图象可知f（

3

2

-1）=f（

1

2

）＜1，故（2）正确；
∵f（0）=1∴f^-1（1）=0，故（3）正确；
原函数在R上单调递减，则反函数在R上单调递减，则f^-1（

1

2

）＞f^-1（1）=0，故（4）正确；
故答案为：（2），（3），（4）

点评：本题主要考查了通过函数图象判定函数性质，以及反函数，属于基础题．