题目内容
已知函数y=f(x)是定义在R上的增函数,且函数y=f(x-1)的图象关于点(1,0)对称,如果实数m,n满足不等式组
,那么m2+n2的取值范围是( )
|
分析:利用条件可得出函数的奇偶性,进而再利用其单调性即可得出m、n的取值范围,再画出图象,根据
表示的几何意义即可求出其取值范围.
| m2+n2 |
解答:解:∵函数y=f(x-1)的图象关于点(1,0)对称,∴函数y=f(x)关于原点对称,即为奇函数;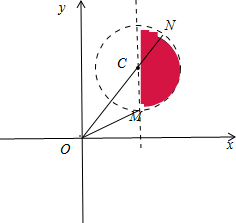
∴由f(m2-6m+21)+f(n2-8n)<0得f(m2-6m+21)<-f(n2-8n)=f(-n2+8n)
又∵函数y=f(x)是定义在R上的增函数,
∴m2-6m+21<-n2+8n,
∴(m-3)2+(n-4)2<4.
∵实数m,n满足不等式组
,即满足
.
作出图象,即图中的阴影部分所表示的点.
∵
表示的是阴影部分的点到原点的距离,
∴|PM|<
<|OC|+r,
求出M(3,2).
∴
<
<
+2
∴13<m2+n2<49.
故选B.

∴由f(m2-6m+21)+f(n2-8n)<0得f(m2-6m+21)<-f(n2-8n)=f(-n2+8n)
又∵函数y=f(x)是定义在R上的增函数,
∴m2-6m+21<-n2+8n,
∴(m-3)2+(n-4)2<4.
∵实数m,n满足不等式组
|
|
作出图象,即图中的阴影部分所表示的点.
∵
| m2+n2 |
∴|PM|<
| m2+n2 |
求出M(3,2).
∴
| 32+22 |
| m2+n2 |
| 32+42 |
∴13<m2+n2<49.
故选B.
点评:由函数的奇偶性和单调性正确得出m、n的取值范围及根据条件作出图形是解题的关键.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足