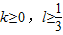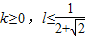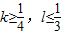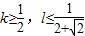题目内容
若对任何x∈[0,1],不等式1-kx≤
≤1-lx恒成立,则一定有( )
| 1 | ||
|
A、k≥0,l≥
| ||||||
B、k≥0,l≤
| ||||||
C、k≥
| ||||||
D、k≥
|
分析:作为选择题可选用特殊值法如k=-1时,由1-kx=1+x≥1,
≤1原不等式不恒成立,可排除A,B,再取k=
时,1-kx=1-
x∈[
,1],
∈ [
,1]原不等式不恒成立,可排除C,从而得到结果.
| 1 | ||
|
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 | ||
|
| 1 |
| 2 |
解答:解:当k=-1时,∵1-kx=1+x≥1,
≤1
∴不等式1-kx≤
≤1-lx不恒成立,可排除A,B
当k=
时,1-kx=1-
x∈[
,1],
∈ [
,1]
不等式1-kx≤
≤1-lx不恒成立,可排除C
故选D
| 1 | ||
|
∴不等式1-kx≤
| 1 | ||
|
当k=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 | ||
|
| 1 |
| 2 |
不等式1-kx≤
| 1 | ||
|
故选D
点评:本题主要考查不等式恒成立问题,作为客观题可灵活地选择方法,提高学习效率,培养学生的能力.

练习册系列答案
相关题目
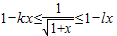 恒成立,则一定有( )
恒成立,则一定有( )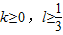
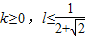
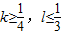
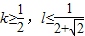
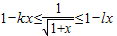 恒成立,则一定有( )
恒成立,则一定有( )