题目内容
14．若做直线运动的物体在[t0，t0+△t]时间内位移的变化量△s=t03△t-3t02△t2+△t3，则该物体在t=t0时的瞬时速度v=t03．分析 由题意知，先计算出平均速度$\overline{v}$的化简式，再由导数的物理意义求出导数即可得到瞬时速度
解答 解：∵做直线运动的物体在[t0，t0+△t]时间内位移的变化量△s=t03△t-3t02△t2+△t3
∴$\overline{v}$=$\frac{△s}{△t}$=t03-3t02△t+△t2，
∴$\underset{lim}{△t→0}$（t03-3t02△t+△t2）=t03，
故答案为：t03．
点评 本题考查函数的平均变化率公式，注意平均速度与瞬时速度的区别，属基础题．
练习册系列答案
相关题目
2．下面各向量中，与向量$\overrightarrow{m}$=（3，2）垂直的是（ ）
| A． | $\overrightarrow{a}$=（2，3） | B． | $\overrightarrow{b}$=（-4，6） | C． | $\overrightarrow{c}$=（3，2） | D． | $\overrightarrow{d}$=（-3，-2） |
9．各项均为正数的数列{an}满足：na2n+1=（n+1）a2n+anan+1，且a3=$\frac{3π}{4}$，若Sn为数列{an}的前n项和，则tanS2015等于（ ）
| A． | -$\sqrt{3}$ | B． | -1 | C． | 0 | D． | 1 |
6．已知f（x）=ax（a＞0且a≠1），若f（-3）＞f（-π）则a的取值范围是（ ）
| A． | a＞0 | B． | a＞1 | C． | a＜0 | D． | 0＜a＜1 |
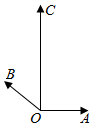如图，已知|$\overrightarrow{OA}$|=1，|$\overrightarrow{OB}$|=2，|$\overrightarrow{OC}$|=6，∠AOB=120°，$\overrightarrow{OA}$•$\overrightarrow{OC}$=0，设$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$（λ、μ∈R），则λ+3μ=8$\sqrt{3}$．