题目内容
8.已知关于x的不等式|2x+1|-|x-1|≤log2a(其中a>0).(1)当a=4时,求不等式的解集;
(2)设f(x)=|2x+1|-|x-1|,若不等式f(x)≤log2a有解,求实数a的取值范围.
分析 (1)把要求的不等式等价转化为与之等价的3个不等式组,求得每个不等式组的解集,再取并集,即得所求.
(2)由(1)求得f(x)的最小值为$-\frac{3}{2}$.所以若使f(x)≤log2a有解,只需log2a≥f(x)min ,由此求得a的范围.
解答 解:(1)当a=4时,f(x)=|2x+1|-|x-1|=$\left\{\begin{array}{l}{-x-2,x<-\frac{1}{2}}\\{3x,-\frac{1}{2}≤x≤1}\\{x+2,x>1}\end{array}\right.$,
不等式即f(x)≤2,可得$\left\{\begin{array}{l}{x<-\frac{1}{2}}\\{-x-2≤2}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{-\frac{1}{2}≤x≤1}\\{3x≤2}\end{array}\right.$ ②,或$\left\{\begin{array}{l}{x>1}\\{x+2≤2}\end{array}\right.$③.
解①求得-4≤x<-$\frac{1}{2}$;解②取得-$\frac{1}{2}$≤x≤$\frac{2}{3}$;解③求得x∈∅,
综上可得,不等式的解集为{x|-4≤x≤$\frac{2}{3}$}.
(2)由(1)可得$f(x)∈[{-\frac{3}{2},+∞})$,
即f(x)的最小值为$-\frac{3}{2}$.所以若使f(x)≤log2a有解,只需log2a≥f(x)min=-$\frac{3}{2}$,
∴a≥${2}^{-\frac{3}{2}}$=$\frac{1}{\sqrt{8}}$=$\frac{\sqrt{2}}{4}$,即a的范围为[$\frac{\sqrt{2}}{4}$,+∞).
点评 本题主要考查绝对值不等式的解法,分段函数的应用,函数的能成立问题,体现了转化、分类讨论的数学思想,属于中档题.

| A. | $\frac{1}{15}$ | B. | $\frac{1}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
| A. | [0,1) | B. | [0,1] | C. | (0,1) | D. | [-1,2) |
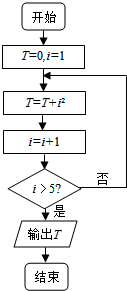
| A. | 30 | B. | 54 | C. | 55 | D. | 91 |
