Question

18．已知地球的半径为R，在南纬α的纬度圈上有A、B两点，若沿纬度圈这两点间的距离为πRcosα，则A、B两点间的球面距离为（π-2α）R．

Answer 1

分析 先求出南纬α的纬度圈所在圆的半径，A、B两地在南纬α的纬度圈上对应的圆心角，得到线段AB的长，利用余弦定理求出∠AOB的大小，利用弧长公式求A、B这两地的球面距离．

解答 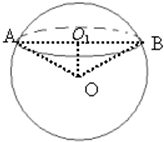解：如图，∵南纬α的纬度圈上有A、B两点，
∴r=O₁A=Rcosα，
∴Rcosα•∠AO₁B=πRRcosα，
∴∠AO₁B=π，
∴AB=2Rcosα．
△AOB中，AB=2Rcosα，OA=R，OB=R，
∴cos∠AOB=$\frac{{R}^{2}+{R}^{2}-4{R}^{2}co{s}^{2}α}{2{R}^{2}}$=1-2cos²α=-cos2α=cos（π-2α），
∴∠AOB=π-2α，
∴A、B两点间的球面距离为l=（π-2α）R．
故答案为：（π-2α）R．

点评 本题考查球的有关经纬度知识，球面距离，弧长公式，考查空间想象能力，逻辑思维能力，是基础题．