题目内容
【题目】已知函数![]() ,
,![]() ,若函数
,若函数![]() 有3个不同的零点x1,x2,x3(x1<x2<x3),则
有3个不同的零点x1,x2,x3(x1<x2<x3),则![]() 的取值范围是_________.
的取值范围是_________.
【答案】![]()
【解析】
先根据题意,求出![]() 的解得
的解得![]() 或
或![]() ,然后求出f(x)的导函数,求其单调性以及最值,在根据题意求出函数
,然后求出f(x)的导函数,求其单调性以及最值,在根据题意求出函数![]() 有3个不同的零点x1,x2,x3(x1<x2<x3),分情况讨论求出
有3个不同的零点x1,x2,x3(x1<x2<x3),分情况讨论求出![]() 的取值范围.
的取值范围.
解:令t=f(x),函数![]() 有3个不同的零点,
有3个不同的零点,
即![]() +m=0有两个不同的解,解之得
+m=0有两个不同的解,解之得![]()
即![]() 或
或![]()
因为![]() 的导函数
的导函数
![]() ,令
,令![]() ,解得x>e,
,解得x>e,![]() ,解得0<x<e,
,解得0<x<e,
可得f(x)在(0,e)递增,在![]() 递减;
递减;
f(x)的最大值为![]() ,且
,且![]()
且f(1)=0;
要使函数![]() 有3个不同的零点,
有3个不同的零点,
(1)![]() 有两个不同的解,此时
有两个不同的解,此时![]() 有一个解;
有一个解;
(2)![]() 有两个不同的解,此时
有两个不同的解,此时![]() 有一个解
有一个解
当![]() 有两个不同的解,此时
有两个不同的解,此时![]() 有一个解,
有一个解,
此时![]() ,不符合题意;
,不符合题意;
或是![]() 不符合题意;
不符合题意;
所以只能是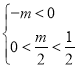 解得
解得![]()
![]() ,
,![]()
此时![]() =-m,
=-m,
此时![]()
![]() 有两个不同的解,此时
有两个不同的解,此时![]() 有一个解
有一个解
此时![]() ,不符合题意;
,不符合题意;
或是![]() 不符合题意;
不符合题意;
所以只能是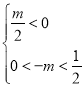 解得
解得![]()
![]() ,
,![]()
此时![]() =
=![]() ,
,
![]()
综上:![]() 的取值范围是
的取值范围是![]()
故答案为![]()

【题目】随着网络和智能手机的普及与快速发展,许多可以解答各学科问题的搜题软件走红.有教育工作者认为:用搜题软件搜索答案可以起到拓展思路的作用,但是对多数学生来讲,容易产生依赖心理,对学习能力造成损害.为了了解搜题软件在学生中的使用情况,某校对200名本校的高二学生在一周内用搜题软件搜题的次数进行了问卷调查,调查结果如下表:
一周内用搜题软件搜题的次数区间 |
|
|
|
|
|
|
人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将一周内用搜题软件搜题的次数在![]() 的学生评价为“有搜题软件依赖症”,在
的学生评价为“有搜题软件依赖症”,在![]() 的学生评价为“有搜题软件过度依赖症”.
的学生评价为“有搜题软件过度依赖症”.
(1)若在这200名高二学生中男生有90人,且男生中有30人“有搜题软件过度依赖症”,请根据上述表格中的统计数据填写下面的![]() 列联表,并通过计算,判断是否有
列联表,并通过计算,判断是否有![]() 的把握认为该校高二学生是否“有搜题软件过度依赖症”与性别有关;
的把握认为该校高二学生是否“有搜题软件过度依赖症”与性别有关;
有搜题软件依赖症 | 有搜题软件过度依赖症 | 合计 | |
男 | 30 | 90 | |
女 | |||
合计 |
(2)在(1)中“有搜题软件过度依赖症”的学生中,按男女学生比例用分层抽样方法抽出5人,进行手机软件搜题问题交流,再从这5人中随机选出3人作重点发言,求选出的这3人中至少有1名女生的概率.
参考公式: ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
