题目内容
在△ABC中,A(cosθ,sinθ)(0<θ<| π | 2 |
(1)用θ表示△ABC的面积S(θ);
(2)求△ABC面积的最大值;
(3)函数y=S(θ)的图象可由函数y=sinθ的图象经过怎样变换得到.
分析:(1)求出点A(cosθ,sinθ) 到直线BC x+y-1=0的距离d,又 AB=
,由S(θ)=
•AB•d 化简可得S(θ)=sin(θ+
)-
.
(2)由以上可得
<θ+
<
,故当θ+
=
时,smax=
-
.
(3)把y=sinθ的图象向左平移
个单位,再把纵坐标缩短为原来的
,再把图象向下平移
个单位 可得y=S(θ)的图象.
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
(2)由以上可得
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
(3)把y=sinθ的图象向左平移
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
解答:解:(1)BC边所在的直线方程为 x+y-1=0,点A(cosθ,sinθ) 到直线方程 x+y-1=0的距离d
等于
,AB=
,∴△ABC的面积S(θ)=
•AB•d=
=
sin(θ+
)-
,(0<θ<
).
(2)由以上可得
<θ+
<
,故当θ+
=
时,smax=
-
,
即△ABC面积的最大值为
-
.
(3)把y=sinθ的图象向左平移
个单位,可得y=sin(θ+
)的图象,再把纵坐标缩短为原来的
,横坐标不变,
可得y=
sin(θ+
)的图象,再把y=
sin(θ+
)的图象向下平移
个单位,即可得到函数y=S(θ)的图象.
等于
| |cosθ +sinθ-1| | ||
|
| 2 |
| 1 |
| 2 |
| |cosθ +sinθ-1| |
| 2 |
sin(θ+
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
(2)由以上可得
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
即△ABC面积的最大值为
| ||
| 2 |
| 1 |
| 2 |
(3)把y=sinθ的图象向左平移
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
可得y=
| ||
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
点评:本题考查点到直线的距离公式,求三角函数的最值,函数y=Asin(ωx+∅)的图象的变换,求出△ABC的面积S(θ)的解析式,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
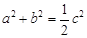 .则直线
.则直线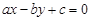 被圆
被圆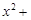
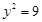 所截得的弦长为 .
所截得的弦长为 .