题目内容
下列说法中:①函数y=lg(x2-ax-a)的值域为R,则a∈(-4,0);
②O是△ABC所在平面上一定点,动点P满足
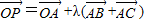 且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;③要得到函数y=f(1-x)的图象只需将y=f(-x)的图象向左平移1个单位;
④若函数
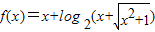 ,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.
,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.其中正确的序号是 .
【答案】分析:①函数y=lg(x2-ax-a)的值域为R,就是g(x)=ax2+ax+1的值域为[0,+∞),根据△≥0,进行求解;
②根据动点P满足 进行移项,发现
进行移项,发现 与
与 的关系进行判断;
的关系进行判断;
③根据平移的性质进行判断,注意“左加右减”;
④已知函数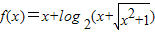 ,证明f(x)是奇函数又是增函数即可证明;
,证明f(x)是奇函数又是增函数即可证明;
解答:解:①∵函数y=lg(x2-ax-a)的值域为R,
可得ax2+ax+1的值域为[0,+∞),
∴△≥0,即(-a)2-4×(-a)=a2+4a≥0,解得a≥0或a≤-4;故①错误;
②O是△ABC所在平面上一定点,动点P满足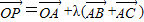 ,
,
∴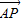 =λ(
=λ( ),说明p在边BC的中线上,λ∈[0,+∞),
),说明p在边BC的中线上,λ∈[0,+∞),
∴P的轨迹一定经过△ABC的重心,故②错误;
③y=f(-x)的图象向左平移1个单位可得y=f[-(x+1)]=f(-x-1),
故③错误;
④因为函数 ,f(-x)=-x+
,f(-x)=-x+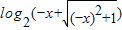
=-[x+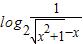 ]
]
=-[ ]=-f(x),f(x)是奇函数,
]=-f(x),f(x)是奇函数,
又f(x)为增函数,∴f(x)在R上是单调增函数,
若“m+n≥0”可得m≥-n,可得f(m)≥f(-n),可得f(m)≥-f(n)即“f(m)+f(n)≥0”;
若“f(m)+f(n)≥0”,可得f(m)≥-f(n)=f(-n),∴m≥-n即m+n≥0,
∴“m+n≥0”是“f(m)+f(n)≥0”的充要条件故④正确.
故④正确,
故答案为:④
点评:此题是一道综合题,考查了二次函数的性质、向量平移的性质、函数的单调性及奇偶性的应用,是一道基础题,难度不大;
②根据动点P满足
 进行移项,发现
进行移项,发现 与
与 的关系进行判断;
的关系进行判断;③根据平移的性质进行判断,注意“左加右减”;
④已知函数
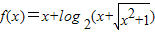 ,证明f(x)是奇函数又是增函数即可证明;
,证明f(x)是奇函数又是增函数即可证明;解答:解:①∵函数y=lg(x2-ax-a)的值域为R,
可得ax2+ax+1的值域为[0,+∞),
∴△≥0,即(-a)2-4×(-a)=a2+4a≥0,解得a≥0或a≤-4;故①错误;
②O是△ABC所在平面上一定点,动点P满足
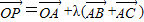 ,
,∴
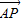 =λ(
=λ( ),说明p在边BC的中线上,λ∈[0,+∞),
),说明p在边BC的中线上,λ∈[0,+∞),∴P的轨迹一定经过△ABC的重心,故②错误;
③y=f(-x)的图象向左平移1个单位可得y=f[-(x+1)]=f(-x-1),
故③错误;
④因为函数
 ,f(-x)=-x+
,f(-x)=-x+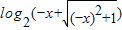
=-[x+
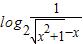 ]
]=-[
 ]=-f(x),f(x)是奇函数,
]=-f(x),f(x)是奇函数,又f(x)为增函数,∴f(x)在R上是单调增函数,
若“m+n≥0”可得m≥-n,可得f(m)≥f(-n),可得f(m)≥-f(n)即“f(m)+f(n)≥0”;
若“f(m)+f(n)≥0”,可得f(m)≥-f(n)=f(-n),∴m≥-n即m+n≥0,
∴“m+n≥0”是“f(m)+f(n)≥0”的充要条件故④正确.
故④正确,
故答案为:④
点评:此题是一道综合题,考查了二次函数的性质、向量平移的性质、函数的单调性及奇偶性的应用,是一道基础题,难度不大;

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
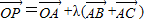 且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;
且λ∈[0,+∞),则P的轨迹一定经过△ABC的内心;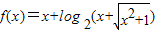 ,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.
,则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.