题目内容
在极坐标中,已知点P为方程ρ(cosθ+sinθ)=1所表示的曲线上一动点Q(2,| π | 3 |
分析:先将原极坐标方程ρ(cosθ+sinθ)=1和点Q(2,
)化成直角坐标方程或直角坐标,再利用直角坐标方程进行求解即得.
| π |
| 3 |
解答:解:将原极坐标方程ρ(cosθ+sinθ)=1,
化为化成直角坐标方程为:x+y-1=0,
点Q(2,
),化成直角坐标为:Q(1,
),
则|PQ|的最小值即为点到直线的距离
d=
=
.
故填:
.
化为化成直角坐标方程为:x+y-1=0,
点Q(2,
| π |
| 3 |
| 3 |
则|PQ|的最小值即为点到直线的距离
d=
| ||
|
| ||
| 2 |
故填:
| ||
| 2 |
点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) 的解集是 .
的解集是 .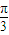 ),则|PQ|的最小值为 .
),则|PQ|的最小值为 .
 的解集是 .
的解集是 .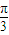 ),则|PQ|的最小值为 .
),则|PQ|的最小值为 .