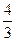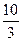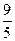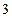题目内容
(11分)
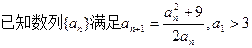
(1)求证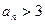 ;
;
(2)比较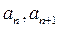 的大小,并证明
的大小,并证明
(3)是否存在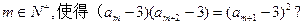 证明你的结论。
证明你的结论。
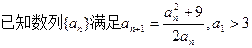
(1)求证
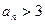 ;
; (2)比较
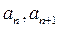 的大小,并证明
的大小,并证明(3)是否存在
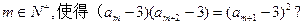 证明你的结论。
证明你的结论。当a1>3时,用数学归纳法证明an>3.
(1)当n=1时不等式成立.
(2)假设当n=k时不等式成立,即ak>3,则
ak+1=>=3,
即当n=k+1时不等式仍成立.
根据(1)和(2),对任何n∈N*,都有an>3.………………………………4分
∵an+1-an=-an=<0,∴an+1<an,n∈N*,………… 7分
(Ⅱ)假设存在使题设成立的正整数m,则
(am-3)(am+2-3)=(am+1-3)2即(am-3)·=(am+1-3)2,
∴am-3=2am+1,即am-3=,从而am=-3,这不可能.
故不存在m∈N*,使得(am-3)(am+2-3)=(am+1-3)2.…………………… 11分
(1)当n=1时不等式成立.
(2)假设当n=k时不等式成立,即ak>3,则
ak+1=>=3,
即当n=k+1时不等式仍成立.
根据(1)和(2),对任何n∈N*,都有an>3.………………………………4分
∵an+1-an=-an=<0,∴an+1<an,n∈N*,………… 7分
(Ⅱ)假设存在使题设成立的正整数m,则
(am-3)(am+2-3)=(am+1-3)2即(am-3)·=(am+1-3)2,
∴am-3=2am+1,即am-3=,从而am=-3,这不可能.
故不存在m∈N*,使得(am-3)(am+2-3)=(am+1-3)2.…………………… 11分
略

练习册系列答案
相关题目
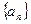 是公差不为零的等差数列,
是公差不为零的等差数列,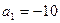 ,且
,且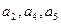 成等比数列.
成等比数列.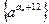 的前n项和公式.
的前n项和公式. ;
;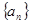 中,已知
中,已知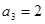 ,
,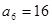 ,则公比
,则公比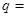 ★ .
★ .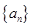 和
和 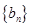 的前n项和分别为
的前n项和分别为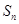 和
和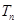 ,且
,且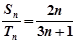 ,则
,则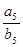 = ( )
= ( )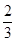
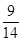
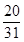
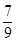
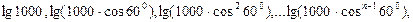 …的前_____项和为最大?
…的前_____项和为最大? 设
设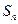 是等差数列
是等差数列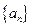 的前
的前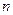 项和,若
项和,若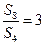 ,则
,则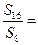 ( )
( )