题目内容
已知定义在R上的函数f(x)=lg(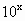 +1)+3x
+1)+3x
(1)设g(x)是R上的奇函数,h(x)是R上的偶函数,且满足f(x)=g(x)+h(x),试求g(x)与h(x);
(2)设a、b∈R,证明a+b>0是f(a)+f(b)>f(-a)+f(-b)的充分必要条件.
答案:
解析:
解析:
|
(1)由f(x)=g(x)+h(x) ∴f(-x)=g(-x)+h(-x). ∵g(x)是奇函数,h(x)是偶函数 ∴f(-x)=-g(x)+h(x) ∴g(x)= g(x)= = = = = h(x)=f(x)-g(x)= (2)任取
∵
∴ 即f(x)是定义域R上的增函数. 由a+b>0,∴a>-b,b>-a. ∴f(a)>f(-b),f(b)>f(-a),将两式相加 ∴f(a)+f(b)>f(-a)+f(-b) 即a+b>0是f(a)+f(b)>f(-a)+f(-b)成立的充分条件. 由f(a)+f(b)>f(-a)+f(-b), ∴g(a)+h(a)+g(b)+h(b)>g(-a)+h(-a)+g(-b)+h(-b). ∵g(a)是奇函数,h(x)是偶函数, ∴g(a)+h(a)+g(b)+h(b)>-g(a)+h(a)-g(b)+h(b). ∴2[g(a)+g(b)]>0. ∴ 即f(a)+f(b)>f(-a)+f(-b)是a+b>0成立的必要条件. 综上,a+b>0是f(a)+f(b)>f(-a)+f(-b)成立的充分必要条件. |

练习册系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |
 [f(x)-f(-x)],h(x)=
[f(x)-f(-x)],h(x)=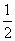 [f(x)+f(-x)].
[f(x)+f(-x)]. +1)+3x-lg(
+1)+3x-lg(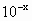 +1)+3x].
+1)+3x].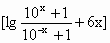

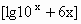
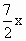 .
.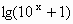 +3x-
+3x-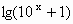 -
-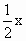 .
.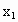 <
<
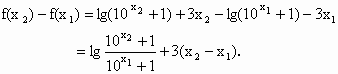
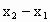 >0.
>0.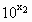 >
>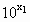 ,
,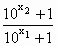 >1,
>1,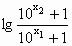 >0
>0 -
-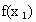 >0,
>0,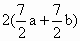 >0,即a+b>0.
>0,即a+b>0.