题目内容
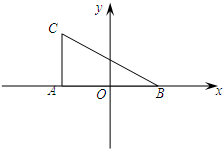 如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=
如图,在Rt△ABC中,∠CAB=90°,|AB|=2,|AC|=| 3 |
| 2 |
(1)求曲线E的方程;
(2)已知点S(0,-
| 3 |
| 3 |
(3)若点F(1,
| 3 |
| 2 |
分析:(1)设P(x,y),由|PA|+|PB|=|CA|+|CB|=
+
=4>2=|AB|,知动点P的轨迹为以A,B为焦点的椭圆,且a=2,c=1,b=
,由此能求出曲线E的方程.
(2)设P(x0,y0)是曲线E上的任意一点,则有
+
=1,y02=3(1-
).由椭圆的对称性设点P在y轴右侧,即0<x0≤2,则kPS=
,kPT=
,由到角公式得tan∠SPT=
=
=
=
=
>0.由此能求出∠SPT的最小值.
(3)由M,N是曲线E上不同的两点,设直线FM的方程为y=k(x-1)+
.由
得(4k2+3)x2-4k(2k-3)x+4k2-12k-3=0.由此能够推导出直线MN的斜率为定值.
| 3 |
| 2 |
(
|
| 3 |
(2)设P(x0,y0)是曲线E上的任意一点,则有
| x02 |
| 4 |
| y02 |
| 3 |
| x02 |
| 4 |
y0+
| ||
| x0 |
y0-
| ||
| x0 |
| kPS-kPT |
| 1+kPS•kPT |
| ||||||||
1+
|
2
| ||
| x02+y02-3 |
2
| ||
x02-
|
8
| ||
| x0 |
(3)由M,N是曲线E上不同的两点,设直线FM的方程为y=k(x-1)+
| 3 |
| 2 |
|
解答:解:(1)设P(x,y),∵|PA|+|PB|=|CA|+|CB|=
+
=4>2=|AB|…(1分)
∴动点P的轨迹为以A,B为焦点的椭圆,且a=2,c=1,b=
…(2分)
∴动点P的轨迹方程即曲线E的方程为
+
=1…(3分)
(2)设P(x0,y0)是曲线E上的任意一点,则有
+
=1,∴y02=3(1-
)
由椭圆的对称性不妨设点P在y轴右侧,即0<x0≤2
则kPS=
,kPT=
,由到角公式得…(4分)tan∠SPT=
=
=
=
=
>0
∴∠SPT为锐角…(6分)
∵0<x0≤2,∴当x0=2时,(tan∠SPT)min=4
…(7分)
∴∠SPT的最小值为arctan4
…(8分)
(3)∵M,N是曲线E上不同的两点,且直线FM和FN的倾斜角互补,则直线FM,FN的斜率存在且不为零.
设直线FM的方程为y=k(x-1)+
由
消y,整理得(4k2+3)x2-4k(2k-3)x+4k2-12k-3=0①…(10分)
设M(x1,y1),N(x2,y2),又F(1,
)是直线FM与椭圆的交点,∴方程①的两根为1,x1
由根与系数的关系得x1=
②…(11分)
∵直线FM和FN的倾斜角互补,∴直线FN的斜率为-k,
以-k代替②中的k得x2=
…(12分)
又y1=k(x1-1)+
,y2=-k(x2-1)+
∴y1-y2=k(x1+x2-2)=k•(
-2)=
而x1-x2=
,∴y1-y2=
(x1-x2)
∴直线MN的斜率为定值,其定值为
…(14分)
| 3 |
| 2 |
(
|
∴动点P的轨迹为以A,B为焦点的椭圆,且a=2,c=1,b=
| 3 |
∴动点P的轨迹方程即曲线E的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设P(x0,y0)是曲线E上的任意一点,则有
| x02 |
| 4 |
| y02 |
| 3 |
| x02 |
| 4 |
由椭圆的对称性不妨设点P在y轴右侧,即0<x0≤2
则kPS=
y0+
| ||
| x0 |
y0-
| ||
| x0 |
| kPS-kPT |
| 1+kPS•kPT |
| ||||||||
1+
|
2
| ||
| x02+y02-3 |
2
| ||
x02-
|
8
| ||
| x0 |
∴∠SPT为锐角…(6分)
∵0<x0≤2,∴当x0=2时,(tan∠SPT)min=4
| 3 |
∴∠SPT的最小值为arctan4
| 3 |
(3)∵M,N是曲线E上不同的两点,且直线FM和FN的倾斜角互补,则直线FM,FN的斜率存在且不为零.
设直线FM的方程为y=k(x-1)+
| 3 |
| 2 |
由
|
设M(x1,y1),N(x2,y2),又F(1,
| 3 |
| 2 |
由根与系数的关系得x1=
| 4k2-12k-3 |
| 4k2+3 |
∵直线FM和FN的倾斜角互补,∴直线FN的斜率为-k,
以-k代替②中的k得x2=
| 4k2+12k-3 |
| 4k2+3 |
又y1=k(x1-1)+
| 3 |
| 2 |
| 3 |
| 2 |
| 8k2-6 |
| 4k2+3 |
| -12k |
| 4k2+3 |
而x1-x2=
| -24k |
| 4k2+3 |
| 1 |
| 2 |
∴直线MN的斜率为定值,其定值为
| 1 |
| 2 |
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=